Пусть на комплексной плоскости Cz задана гладкая или кусочно-гладкая кривая 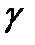 =AB.Если кривая замкнута, то A=B. Установим положительное направление на кривой, считая точку A первой, если кривая незамкнутая. Если кривая замкнута, то положительным направлением обхода будем считать движение против часовой стрелки.
=AB.Если кривая замкнута, то A=B. Установим положительное направление на кривой, считая точку A первой, если кривая незамкнутая. Если кривая замкнута, то положительным направлением обхода будем считать движение против часовой стрелки.
Предположим, на AB задана непрерывная ограниченная функция f(z). Точками
А=z0<z1<z2<zn=B. Кривую АВ разобьем на элементарные дуги 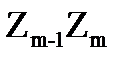 , m=1, 2, 3,… n. Нумерация точек производится в направлении от точки A к В. Обозначим
, m=1, 2, 3,… n. Нумерация точек производится в направлении от точки A к В. Обозначим
DZm = Zm- Zm-1 m=1,2,3,…n. На каждой дуге Zm-1Zm выберем по одной точке 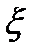 m и образуем сумму
m и образуем сумму
dn= 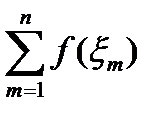
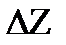 m (26.1)
m (26.1)
Сумма (4.1) называется интегральной суммой Римана для функций f (z) по кривой AB= 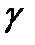 .
.
Определение 26.1 Конечный предел этой суммы при условии, что 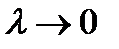 где
где 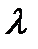 =max|
=max| 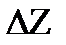 m|, если этот предел не зависит ни от способа разбиения кривой, ни от способа выбора точек
m|, если этот предел не зависит ни от способа разбиения кривой, ни от способа выбора точек 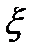 m. называется интегралом от функций f (z) по кривой
m. называется интегралом от функций f (z) по кривой 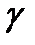 и обозначается
и обозначается
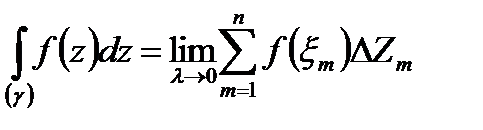 (26.2)
(26.2)
При этом функция f(z) называется интегрируемой по кривой 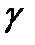 .
.
Пусть z=x+iy, f(z)=U(x,y)+iV(x,y)
Введем обозначения Zm= х m+i y m хm- хm-1=  хm
хm
уm- уm-1=  уm,
уm, 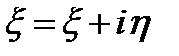
Тогда 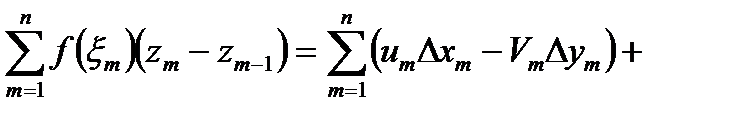
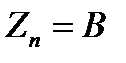
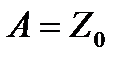
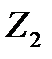
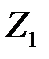 +
+ 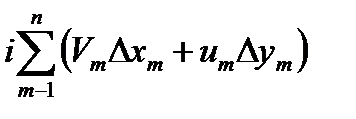
Где 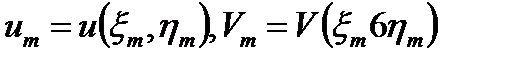
Переходя в этом равенстве к пределу, при l  , получаем
, получаем
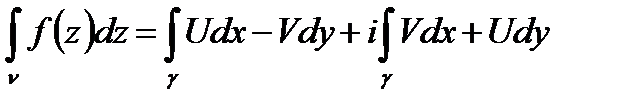 (26.3)
(26.3)
Следовательно, существование интеграла 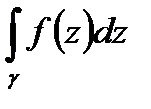 равносильно существованию следующих двух криволинейных интегралов от действительных функций:
равносильно существованию следующих двух криволинейных интегралов от действительных функций:
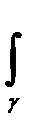 Udx-Vdy,
Udx-Vdy, 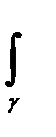 Vdx+Udy
Vdx+Udy
Если кривая 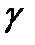 задана параметрическим уравнением
задана параметрическим уравнением
Z= 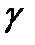 (t) =
(t) = 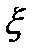 (t) +i
(t) +i  (t), a
(t), a 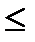 t
t 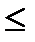
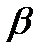 ,
,
то в формуле (26.3)
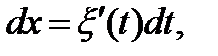
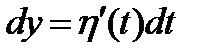 и, следовательно,
и, следовательно,
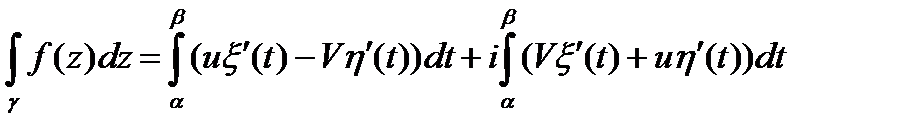
(26.4.)
Пример 26.1. Пусть f(z)=1. A и B- соответственно начало и конец кривой 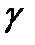 . Тогда интегральная сумма (26.1) равна
. Тогда интегральная сумма (26.1) равна
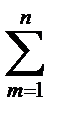 (zm-zm-1)=z1-z0+z2-z1...+zn-zn-1=zn-z0=B-A
(zm-zm-1)=z1-z0+z2-z1...+zn-zn-1=zn-z0=B-A
Откуда 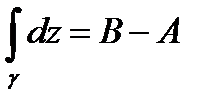 . Таким образом,
. Таким образом, 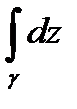 зависит только от начальной и конечной точке кривой
зависит только от начальной и конечной точке кривой 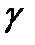 и не зависит от пути интегрирования.В этом случае вместо
и не зависит от пути интегрирования.В этом случае вместо 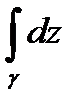 можно записать
можно записать 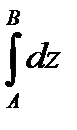 . В частности, если A=B то
. В частности, если A=B то 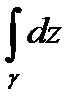 =0, т.е. интеграл
=0, т.е. интеграл 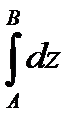 по любой замкнутой кривой равен нулю.
по любой замкнутой кривой равен нулю.
 2015-03-07
2015-03-07 373
373








