В общем случае интеграл 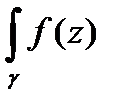 dz зависит от пути интегрирования, а не только от начальной и конечной точки. Выясним условия, при которых интеграл от формы пути не зависит.
dz зависит от пути интегрирования, а не только от начальной и конечной точки. Выясним условия, при которых интеграл от формы пути не зависит.
Ответ на этот вопрос содержится в следующей теореме.
Теорема.26.1. Если функция f(z) аналитична в односвязной области D, то интеграл от этой функции вдоль всякого замкнутого кусочно- гладкого контура g, целиком лежащего в D, равен нулю.
Доказательство. Пусть f(z)=u(x,y)+iv(x,y) аналитическая в области D функция. Напомним, что функции u(x,y), v(x,y) имеет в этой области частные производные
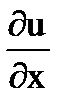 ,
, 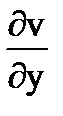 ,
, 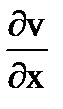 ,
, 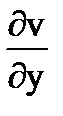
Через g обозначим любой замкнутый контур целиком лежащий в D. Имеем
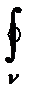 f(z)dz=
f(z)dz= 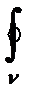 u(x)dx-Vdy+i
u(x)dx-Vdy+i 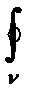 Vdx+udy (26.8)
Vdx+udy (26.8)
Из условии Коши-Римана следует
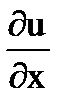 =-
=- 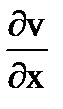
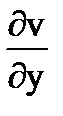 =
= 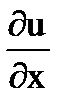
Этих условий и непрерывности функций 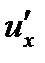 ,
, 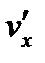 ,
, 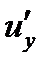 ,
, 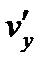 достаточно для обращения интегралов в соотношении (26.8) в нуль.
достаточно для обращения интегралов в соотношении (26.8) в нуль.
Теорема.26.2. Если F(z) аналитична в односвязной области D, то интеграл
I= 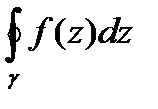
не зависит от формы пути интегрирования g=AB для любых точек А и В из D.
Действительно, если дуги C1 и C2 имеют общую начальную точку A и общую конечную точку B, то
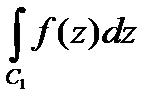 -
- 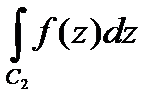 =0.
=0.
По теореме 26.1
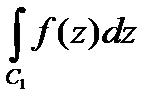 =
= 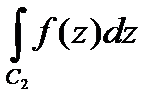
Если интеграл не зависит от формы пути AB, то используют обозначения
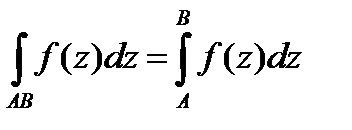
 2015-03-07
2015-03-07 1858
1858
