Из формулы (26.3) следует, что непрерывная на кривой функция интегрируема на этой кривой. Из свойств криволинейных интегралов вытекает так же, что имеют место следующие формулы:
1. 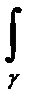 [ а f(z)+bg(z)]dz=
[ а f(z)+bg(z)]dz= 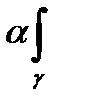 f(z)dz+b
f(z)dz+b 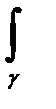 g(z)dz, (26.5)
g(z)dz, (26.5)
где а и в – любое комплексные числа (линейность интеграла)
2. 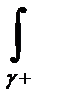 f(z)dz= -
f(z)dz= - 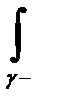 f(z)dz (26.6)
f(z)dz (26.6)
т.е. при изменении ориентации кривой интеграл меняет знак.
3. 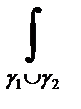 f(z)dz=
f(z)dz= 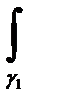 f(z)dz+
f(z)dz+ 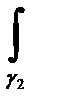 f(z)dz (26.7)
f(z)dz (26.7)
4. | 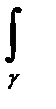 f(z)dz|£
f(z)dz|£ 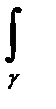 |f(z)| dz
|f(z)| dz
Пример 26.2. Пусть f(z)=Z, 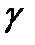 -кривая с началом в точке A и концом в точке B. Так как функция f(z)=Z непрерывна на кривой
-кривая с началом в точке A и концом в точке B. Так как функция f(z)=Z непрерывна на кривой 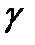 , то интеграл
, то интеграл 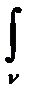 zdZ существует. предел (26.2) не зависит от выбора точек
zdZ существует. предел (26.2) не зависит от выбора точек 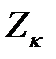 ,
, 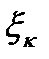 . Положим
. Положим
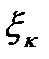 = Zk-1, тогда
= Zk-1, тогда 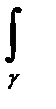 zdz=
zdz= 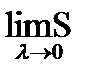 , где
, где
S= 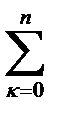 Zk-1(Zk-Zk-1). Полагая
Zk-1(Zk-Zk-1). Полагая 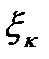 =Zk, получаем
=Zk, получаем 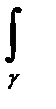 zdz=
zdz= 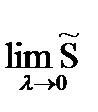 , где
, где
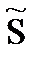 =
= 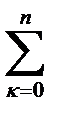 Zk(Zk-Zk-1)
Zk(Zk-Zk-1)
Следовательно, 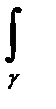 zdz=(1/2)
zdz=(1/2) 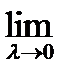 (S +
(S + 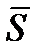 ),
),
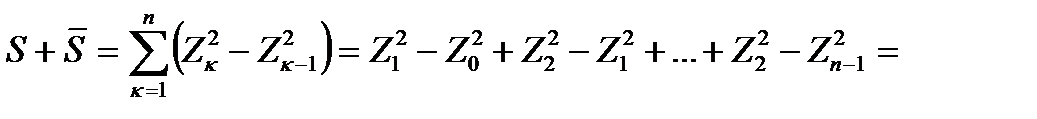 =
= 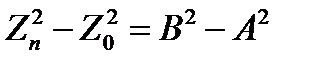
Откуда находим
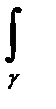 zdz=
zdz= 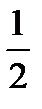 (B2-A2)
(B2-A2)
Таким образом, интеграл 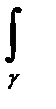 zdz не зависит от пути интегрирования. В частности, интеграл
zdz не зависит от пути интегрирования. В частности, интеграл 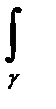 zdz по любой замкнутой кривой равен нулю.
zdz по любой замкнутой кривой равен нулю.
Пример.26.3. Вычислить интеграл
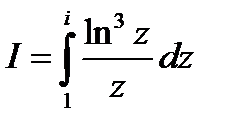
По дуге окружности |z|=1 (lnz - главное значение логарифма ln1=0)
Решение. Первый способ. Применяя формулу Ньютона-Лейбница, получим:
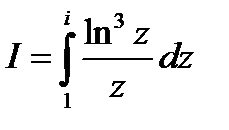 =
= 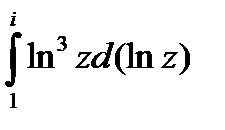 =
= 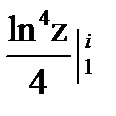 =
= 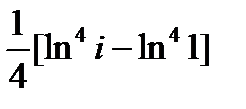 = =
= = 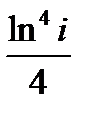 =
= 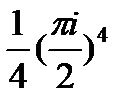 =
= 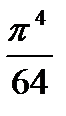 ;
;
|
|
|
Второй способ. Делаем замену переменной
lnz=W, dW= 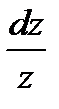
Дуга окружности, z=1 переходит в отрезок мнимой оси заключенной между точками (0, 0) и (0, 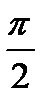 ).
).
Интеграл примет вид
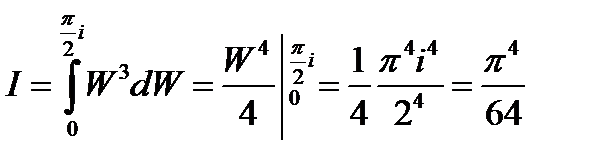 ;
;
Третий способ. Положим
z=e ij (Здесь r=|z|=1),
тогда lnz=ij, dz=ieijdj
Действительная переменная  изменяется в пределах 0<
изменяется в пределах 0<  <
< 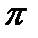 /2. В этом случае получаем
/2. В этом случае получаем
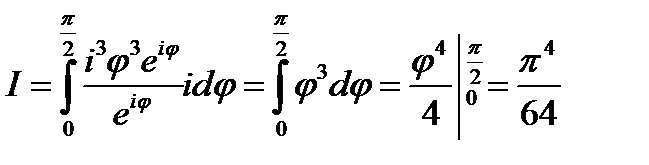 ;
;
 2015-03-07
2015-03-07 459
459








