Пусть дана квадратная матрица А порядка n.
Обратной матрицей по отношению к данной А называется матрица 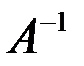 , которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
, которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
По определению
А · 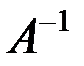 =
= 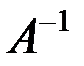 · А = Е.
· А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
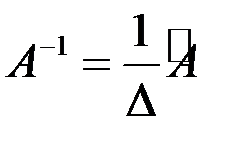 ,
,
где 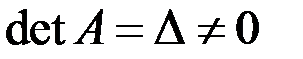 - определитель матрицы А,
- определитель матрицы А, 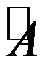 - союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
- союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
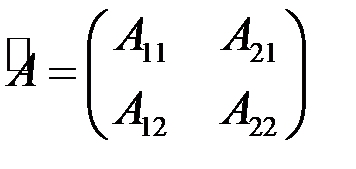 ,
,
для квадратной матрицы 3-го порядка союзной является матрица
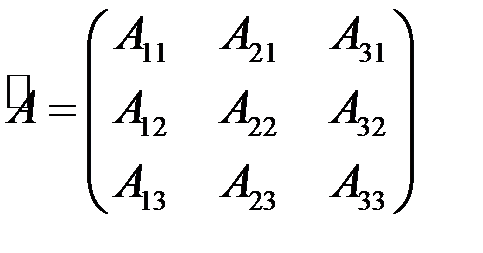 .
.
Пример
Для матрицы 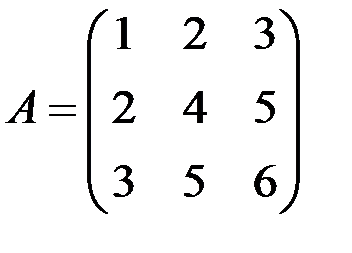 найти обратную.
найти обратную.
Решение
Обратную матрицу находим по формуле
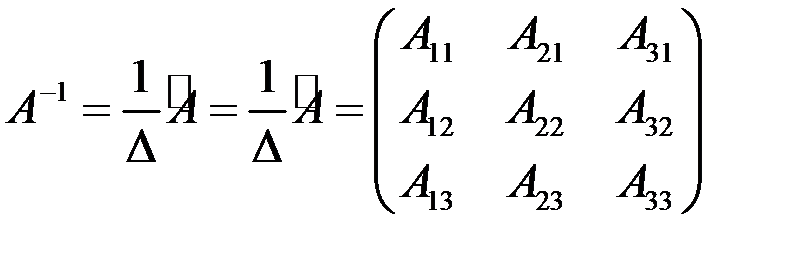 .
.
Определитель матрицы 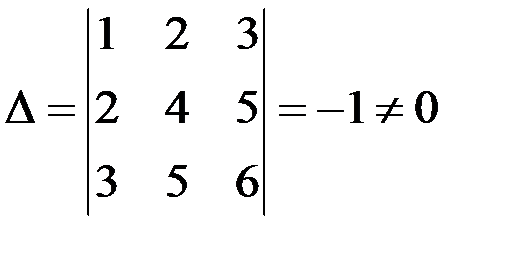 , следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
|
|
|
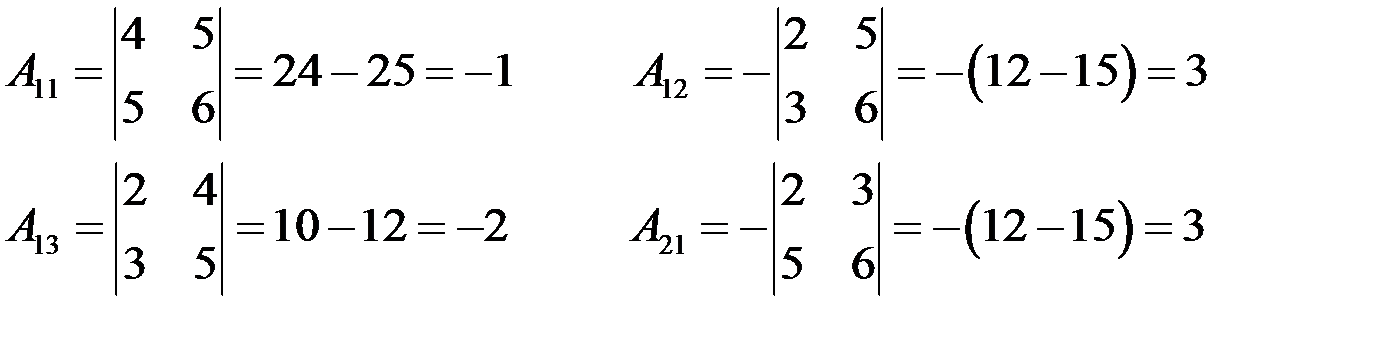
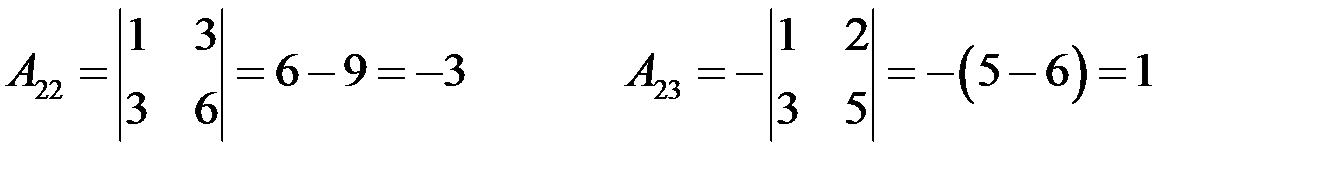
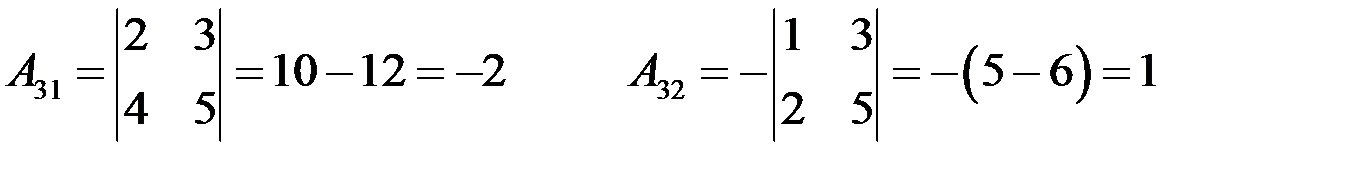
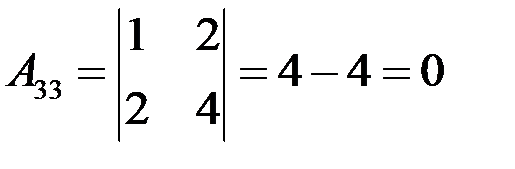 .
.
Тогда обратная матрица имеет вид
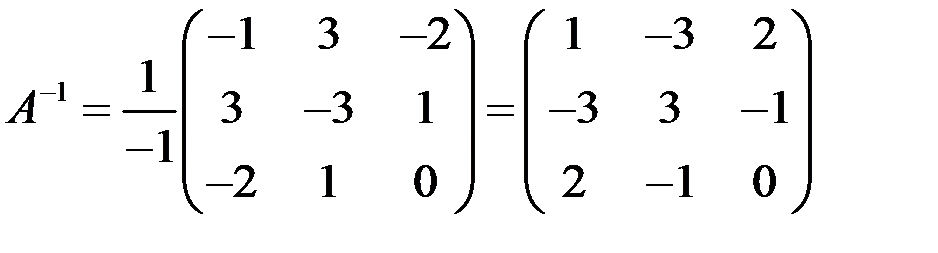 .
.
 2015-03-07
2015-03-07 983
983








