Функция 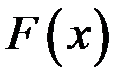 называется первообразной для функции
называется первообразной для функции 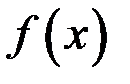 на интервале
на интервале 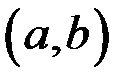 , конечном или бесконечном, если в любой точке
, конечном или бесконечном, если в любой точке 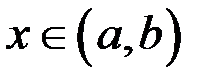 этого интервала функция
этого интервала функция 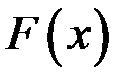 дифференцируема и имеет производную
дифференцируема и имеет производную 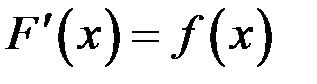 .
.
Совокупность всех первообразных для функции 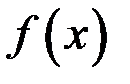 , определенных на интервале
, определенных на интервале 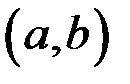 , называется неопределенным интегралом от функции
, называется неопределенным интегралом от функции 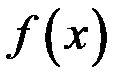 на этом интервале и обозначается символом
на этом интервале и обозначается символом
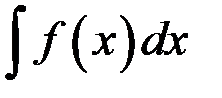 .
.
Метод подведения под знак дифференциала следует из свойства инвариантности неопределенного интеграла.
Пусть дан интеграл 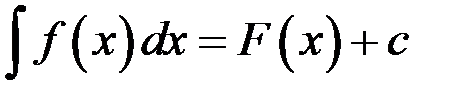 . Справедливо равенство
. Справедливо равенство
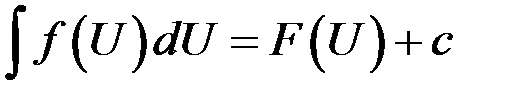 ,
,
где 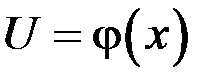 – некоторая непрерывно дифференцируемая функция.
– некоторая непрерывно дифференцируемая функция.
Таблица интегралов
1. 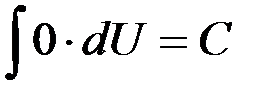 | 8. 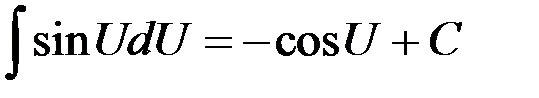 |
2. 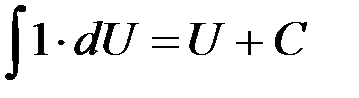 | 9. 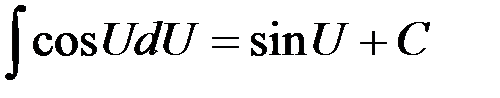 |
3. 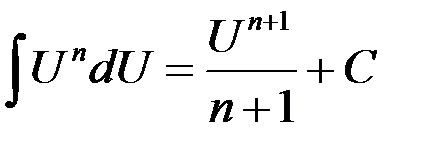 | 10. 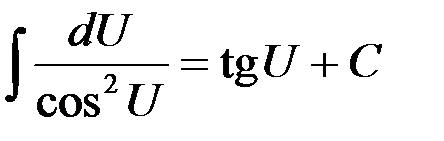 |
4. 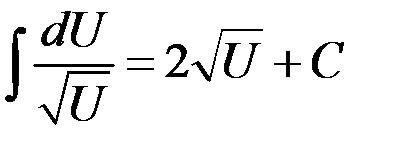 | 11. 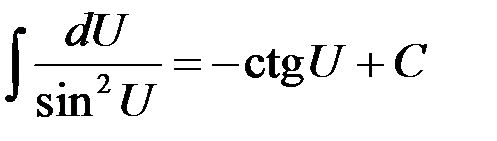 |
5. 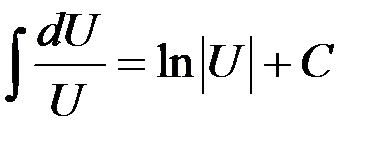 | 12. 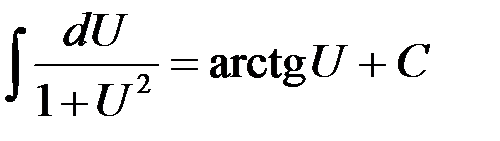 |
6. 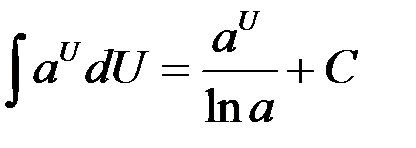 | 13. 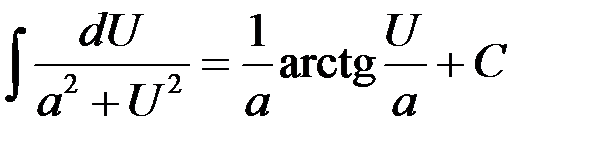 |
7. 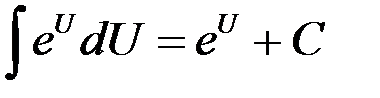 | 14. 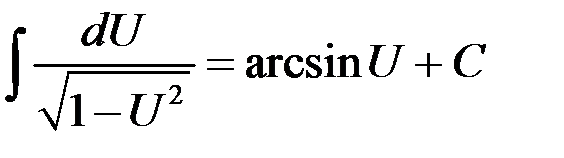 |
15. 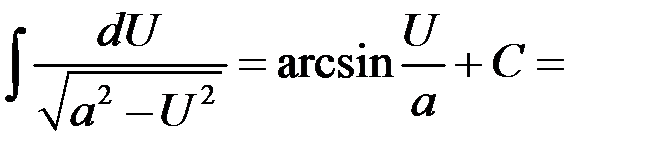 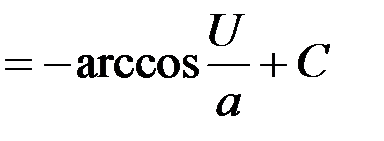 |
При интегрировании методом подведения под знак дифференциала необходимо иметь в виду следующие равенства:
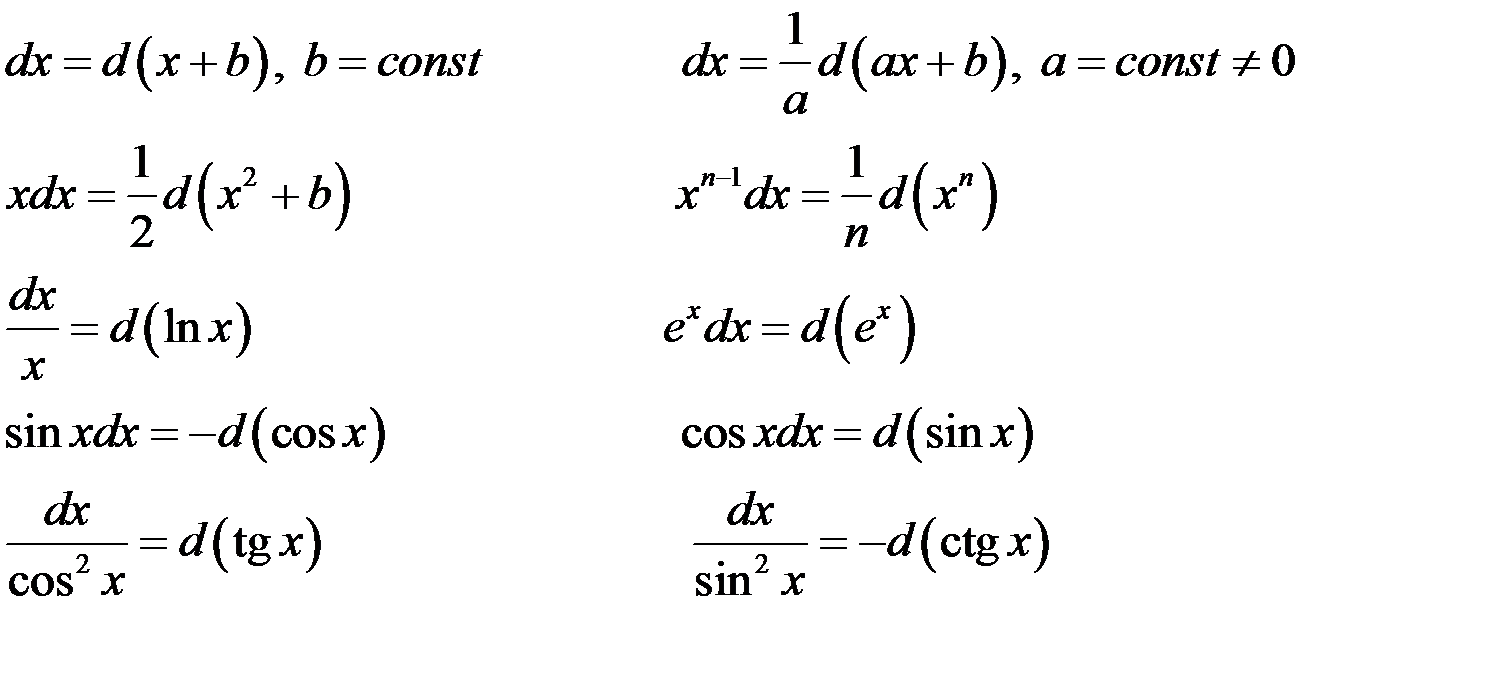
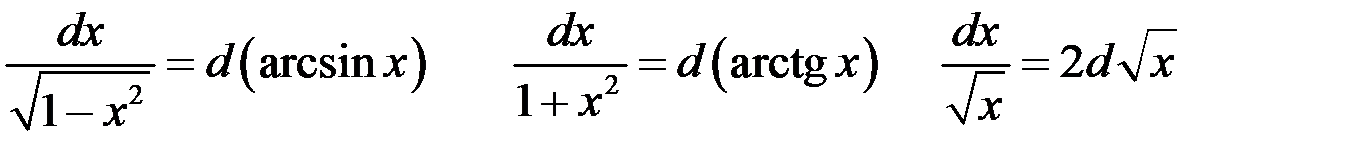
В общем случае
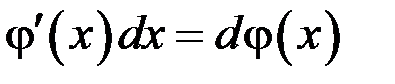 .
.
 2015-03-07
2015-03-07 1529
1529








