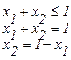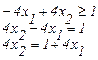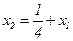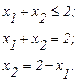2015-03-27
748
Область допустимых решений D в задаче ЛП образуется путём пересечения m полупространств, каждая из которых определяется соответственно. Линейным неравенством (ограничением) модели из области D:
; 
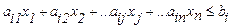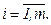(2.5)
Пересечением указанных полупространств является выпуклый прямоугольник.
При этом множество значений х, удовлетворяющих неравенствам (ограничениям) модели, может быть: пустым (рис.2.2а), ограниченным (рис. 2.2б), неограниченным (рис.2.2в).
В первом случае задача не имеет решения, т.к. система линейных неравенств противоречива.
Рассмотрим целевую функцию:
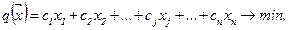(2.6)
пусть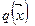 
= const, тогда:
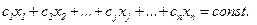(2.7)
а) б) в) г)
Рис. 2.2
Изобразив геометрически целевую функцию, получим плоскость, в пределах которой значения функции будут одинаковы и равны заданной const.
Следует помнить, что её нормальный вектор будет указывать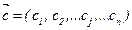 
направление улучшения линейной функции 
.
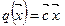Будем перемещать плоскость 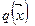= const, чтобы она оставалась перпендикулярна вектору 
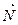. При этом возможны следующие случаи:
а) плоскость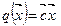 
= const и область D будут иметь лишь одну общую точку - вершину многогранника, определяющую единственное решение модели ЛП;
|
|
|
б) плоскость 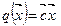=const и область D имеют целое множество общих точек - плоскость целевой функции совпадает с ребром или гранью многогранника (в случае их параллельности плоскости), определяющие бесчисленное множество решений.
Таким образом, можно сделать следующие выводы:
- решение задачи ЛП, если оно существует, не может лежать внутри области допустимых решений D, а только на её грани;
- решение задачи ЛП, минимизирующее функцию 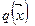(оптимальное решение), всегда достигается в одной из вершин многогранника допустимых решений (если оно достигается на целой границе или ребре, то оно же достигается и в каждой из вершин, через которые проходит эта грань или ребро).
- для того, чтобы найти оптимальное решение, достаточно сделать перебор всех вершин многогранника и выбрать из них ту, в которой функция достигает своего минимума.
2.2 Пример решения задачи скалярной оптимизации
графическим методом
Постановка задачи: Найти минимум функции двух переменных, поиск решения на области допустимых решений D, которая образована следующими неравенствами [23]:……..
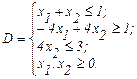(2.8)
Критерий оптимизации: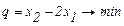 
.
Строим систему координат x10x2.
Так как из условия (2.8) х1≥0 и х2≥0, то область D принадлежит первому квадранту.
Первый этап графического решения - изображение на плоскости области D.
Рассмотрим последовательно все условия (табл. 1.6).
Выбираем другое значение q, но с учётом того, что целевая функция стремится к минимуму (т.е. выберем значение меньше, чем было изначально).
Пусть q=0, т.е. строим линию, это линия уровня при q=0:
|
|
|
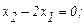(2.8)
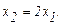(2.9)
| х1 | ||
| х2 |
Таблица 1.6
Условие 1
D1 -множество точек (x1, x2), удовлетворяющих данному ограничению. Для этого всю плоскость x10x2 разбиваем на множество точек принадлежащих D1 и не принадлежит D1 т.е. когда условие 1 выполняется (принадлежит D1) и не выполняется (не принадлежит D1). Строим границу области D1, и x1+x2= 1 Берём любую точку с координатами (1;1) x1+x2≤ 1 2 ≤ 1 л. | Условие 2
Возьмём точку с координатами (1;1) -4+4≥ 1 0≥ 1 л. вверх от (2) При рассмотрении условия (2) получили область D2, штрихуем. | Условие 3
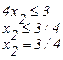получаем прямую параллельную оси
Возьмём точку с координатами (1;1)
4·1≤ 3
4 ≤ 3 (л.)
Вниз от (3)
При рассмотрении условия (3) получили область D3, штрихуем.
|
Построены две линии уровня, причем они параллельны между собой. При переходе от линии q=2 к линии q=0 целевая функция уменьшается и т.к. надо найти минимум, то, следовательно, она улучшается, т.е. при перемещении линии уровня в направлении, указанном стрелками - целевая функция – улучшается, а это направление и есть направление вектора градиента.
Для решения задачи ЛП надо найти такую точку, чтобы она лежала в области D (прямоугольника ABCD) и при этом через неё проходила линия уровня с минимальным значением q. Очевидно, что построенная линия q=0, не является оптимальной, этим свойством будет обладать линия, проходящая через точку D.
Аналитически определить координаты точки D можно, решив совместно два уравнения для условия (2.8) и условия (2.9).
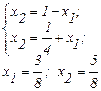(2.10)
Таким образом, точка D имеет координаты (0,375; 0,625) и принадлежит исследуемой области D.
Линия равного уровня, проходящая через эту точку:
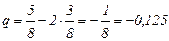- это есть минимальное значение целевой функции.
Таким образом, чтобы графически решить задачу ЛП надо:
1) построить область D;
2) построить линии равного уровня целевой функции (достаточно двух линий) и определить, в какую сторону надо их перемещать, чтобы функция улучшилась;
3) найти крайнюю точку выпуклого многоугольника области D, через которую проходит линия наилучшего уровня.
Иногда линии уровня параллельны какой-нибудь линии ограничения. Тогда оптимальным решением будет не единственное значение, а целый отрезок.
Пример:
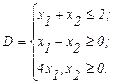(2.11)
| х1 | ||
| х2 | +1 |
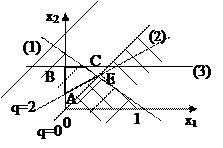
Координаты:
т.А (0;0,25)
т.В (0;0,75)
т.С (0,75;0,75)
т.E (0,375;0,625)
Рис. 2.3 – К решению задачи ЛП
Таким образом, область D - выпуклый четырёхугольник ABCD получили как пересечение подобластей D 1∩ D 2∩ D 3 (рис. 2.3).
Если в условии, которое образует область D, стоит только знак равно, то множество точек, удовлетворяющее ему, не область, лежащая выше или ниже прямой, а сама прямая.
Например: пусть область D задана неравенствами:
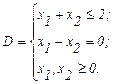(2.12)
Строим область D, рассматривая каждое неравенство в отдельности.
| условие 1 | условие 2 | условие 3 | ||||||
| 
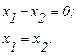Биссектриса I и III квадрантов, точки лежат на самой прямой.
| 
Это I квадрант плоскости х10х2.
|
 |
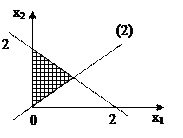Рис. 2.4
В итоге область D это отрезок на прямой x1=x2 из условия (2) внутри области D1.
Второй этап- изображение целевой функции.
Целевая функция - это функция, для которой в задаче надо найти максимум или минимум. Если она зависит от двух переменных х1 и х2, то её изображение на плоскости есть линии равного уровня, т.е. таких линий, в каждой точке которых функция имеет, одинаковое значение.
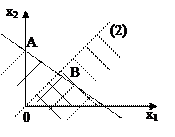
Способ рассмотрения линий равного уровня рассмотрим на примере q= х2-2х1.
Зафиксируем любое значение q, например q=2.
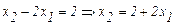. Это прямая, строим её на плоскости:
| х1 | 0 | -1 |
| х2 | 2 | 0 |
и подписываем q=2 это линия уровня, где q=2.
