2015-03-27
431
Симплекс-метод - это численный способ решения задачи линейного программирования. Он основан на следующих высказываниях:
1) Область D допустимых решений задачи ЛП представляет собой выпуклый многогранник в пространстве переменных х1, х2,…,xn;
2) Оптимальное значение целевой функции достигается в одной из угловых точек этого многогранника.
Основная идея метода- перебор угловых точек и выбор лучшей, т.е. той, где целевая функция максимальна или минимальна. Поскольку число угловых точек не бесконечны, то решение симплекс-метода можно получить за конечное число шагов [14].
Ранее мы рассматривали решение задачи ЛП графически. Мы построили на плоскости х10х2 область допустимых решений D - это получился прямоугольник ABCЕ и преобразили линии равного уровня – это графические изображения целевой функции.
Критерии оптимизации: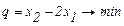 
.
Область допустимых решений:
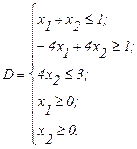(2.13)
Из графического решения имеем координаты вершин выпуклого многоугольника: т. А (0;0,25), т.В (0;0,75), т.С (0,25;0,75), т.Е (0,375;0,625).
Решением была т.E и значение целевой функции в ней
q= -0,125.
Рассмотрим симплекс-метод на примере этой задачи. Последние два условия рассматривать не будем. Приводим задачу к канонической форме, для этого добавляем к левой части вспомогательную неотрицательную переменную со знаком “+”, если неравенство типа меньше и со знаком “-”, если - “больше или равно”:
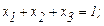(2.14)
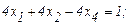(2.15)
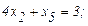(2.16)
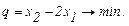(2.17)
Второй этап - составление симплекс-таблиц.
Для этого разбиваем переменные на множества:
1) базисные переменные – их число равно числу ограничений (равно 3);
2) небазисные – все остальные (их будет 5-3=2).
Выразим базисные переменные через небазисные. Следует помнить, что способ разбиения множеств переменных на базисные и небазисные может быть любым, надо только чтобы свободные члены в выражениях q базисных переменных были неотрицательны, т.е.:
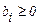. (2.18)
При ручном варианте симплекс-метода разделение делается методом проб и ошибок – сначала попробуем найти выражение, потом смотрим, выполняется ли условие (2.18) и делаем вывод, какие переменные взять в базис.
Из (2.16) выразим х2 и подставим в (2.14) и (2.15):
из (2.16)
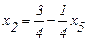, (2.19)
подставим выражение в (2.15):
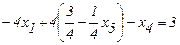; (2.20)
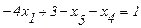; (2.21)
выразим
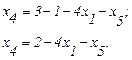(2.22)
(2.19) подставим в (2.14):
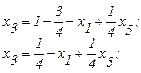(2.23)
(2.19) подставим в целевую функцию:
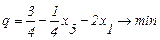. (2.24)
Получим первую симплекс-таблицу, т.е. набор выражений базисных переменных (х2, х3, х4) через небазисные (х1, х5):
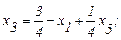(2.25)
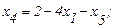(2.26)
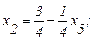(2.27)
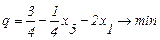(2.28)
Условие (2.18) выполняется, следовательно, данное разбиение допустимо.
Если положить небазисные переменные равными нулю и вычислить значение базисных, то получим базисную точку:
| х1 | х2 | х3 | х4 | х5 | q |
| 3/4 | 1/4 | 3/4 |
На графике (рис. 2.3) точка с координатами (0;0,75) – это точка B - угловая. Можно доказать, что базисная точка всегда является угловой.
Следует помнить, что базисная точка определяется способом разбиения переменных на базисные и небазисные (т.е. если х2, х3, х4 - базисные, то получим точку B). Поэтому, чтобы перейти в другую базисную точку и найти в ней целевую функцию надо по-другому разбить переменные на подмножества.
В симплекс-методе переход к новой базисной (к новому разбиению) делается так: выбирается небазисная переменная и переводится в базис (делается базисной). Чтобы количество базисных переменных не изменилось, какая-то базисная переменная выводится из базиса. Так сделано, чтобы упростить перебор базисных точек (т.е. не все сразу переменные меняются местами, а по одной).
Третий этап - перебор базисных точек.
Чтобы не перебирать точки вслепую, надо следующей точкой выбрать такую, чтобы целевая функция улучшилась, т.е. перебор должен быть направленным.
В новой базисной точке базисной переменной может быть х1 или х5, сейчас х1= х5=0. Если какую-то из них сделать базисной, то она будет положительной. Так как коэффициенты в целевой функции у обеих переменных отрицательны, то при их увеличении значение q уменьшается.
Правило 1:
а) при поиске минимума целевой функции в базис переводят ту переменную, у которой коэффициент в целевой функции максимален по модулю среди отрицательных;
б) при поиске максимума целевой функции – в базис переводят ту переменную, у которой в целевой функции максимальный положительный коэффициент.
Итак делаем базисной х1. Для этого надо выразить её из какого-нибудь уравнения (2.25)–(2.27) и подставить в остальные уравнения целевой функции. Попробуем выразить х1 из (2.26):
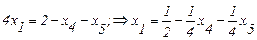. (2.29)
Свободный член 1/2> 0, что допустимо. Подставим в (2.25):
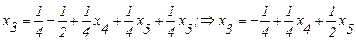. (2.30)
Свободный член -1/4< 0, отрицательный, такое разбиение недопустимо. Пробуем другой вариант.
Выразим х1 из (2.25):
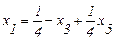. (2.31)
Выражение (2.31) подставим в (2.26):
;
;
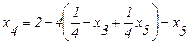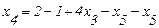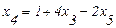. (2.32)
Условие (2.27) остаётся без изменения.
Подставим (2.31) в целевую функцию:
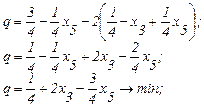(2.33)
получим вторую симплекс-таблицу:
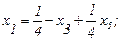(2.35)
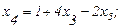(2.36)
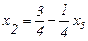; (2.37)
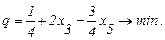(2.38)
Условие (2.18) выполняется.
| х1 | х2 | х3 | х4 | х5 | q |
| 1/4 | 3/4 | 1/4 |
Вторая базисная точка.
В выражении целевой функции переменная х5 имеет отрицательный коэффициент, теперь ее переводим в базис. Выразим х5 из (2.32):
;
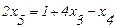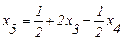. (2.39)
Подставим (2.39) в выражение (2.35):
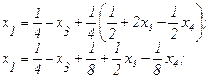
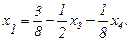(2.40)
Подставим (2.39) в выражение (2.37):
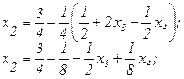
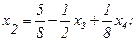(2.41)
Подставим (2.39) в целевую функцию (2.38):
;
;
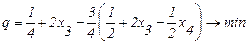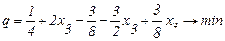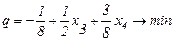. (2.42)
Получим симплекс-таблицу, включающую выражения (2.39)-(2.42).
Условие (2.18) выполняется.
Новая базисная точка:
| х1 | х2 | х3 | х4 | х5 | q |
| 3/8 | 5/8 | 1/2 | -1/8 |
На графике это точка Е с координатами (3/8; 5/8).
Есть ли лучшая базисная точка? Все коэффициенты в целевой функции положительны, следовательно, никаким новым выборам базисной переменной q (целевой функции) нельзя уменьшить, таким образом, найдена оптимальная точка [10].
Правило 2. Критерии окончания поиска решения:
а) если при поиске минимума целевой функции коэффициенты при всех переменных целевой функции положительны, то найдена оптимальная точка.
б) если при поиске максимума целевой функции коэффициенты при всех переменных отрицательны, то найдена оптимальная точка.
