Комбинированные модели, составления из параллельно соединённых зон

На основе материального баланса для точки z (рис. 1.25):

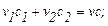(1.43)

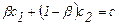; (1.44)

т.е. с=f(c₁,c₂);

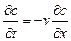. (1.45)

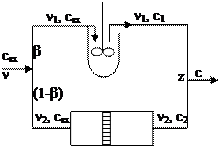Рис. 1.25 – Схема к комбинированной модели

Разделим правую и левую части уравнения на v, приведём задачу к безразличному виду:

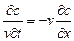, (1.46)

разделим на с₀ и внесём v под знак :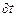

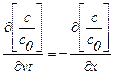, (1.47)

разделим на l и внесем l под знак :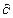

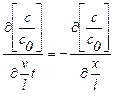. (1.48)

Обозначим:

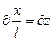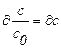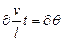; ; . (1.49)

где z - безразмерная координата длины; с – безразмерная координата концентрации; Ө – безразмерная координата времени,

откуда:

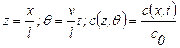. (1.50)

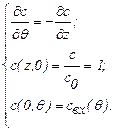(1.51)

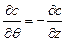. (1.52)

Заменим частные дифференциалы левыми конечными разностями относительно 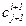[9]:

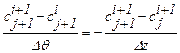; (1.53)

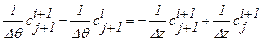_; (1.54)

разделим на :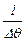

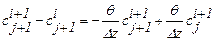; (1.55)

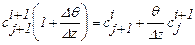; (1.56)

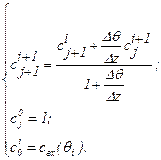(1.57)

При этом начальные и граничные условия имеют следующий вид:

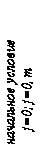
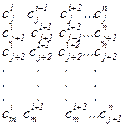(1.60)