Б. Нули аналитической функции

Пусть 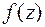– аналитическая в области 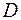функция и .

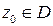Определение. Точка 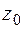называется нулем функции 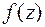, если .

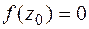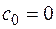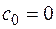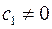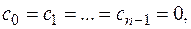
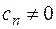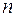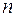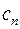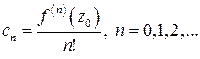Из этого определения следует, что в тейлоровском разложении (1) в окрестности нуля функции коэффициент . Если , но , то имеет в точке простой нуль. Если в (1) , то точка называется нулем - го порядка ( -ой кратности) функции . Так как коэффициенты определяются через производные функции в точке соотношениями , то порядок нуля функции в точке равен порядку младшей отличной от нуля производной (если – конечная точка плоскости).

Для того чтобы точка была нулем 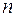-го порядка аналитической в этой точке функции , необходимо и достаточно, чтобы в некоторой окрестности этой точки имело место представление

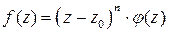, (6)

где 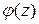– аналитическая в точке функция и .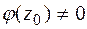

В случае, когда нулем функции является бесконечно удаленная точка, то есть 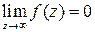, представление (6) принимает вид

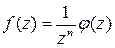, (7)

где 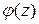– аналитическая в окрестности бесконечно удаленной точки функция и 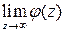есть конечное отличное от нуля число.

Пример 6. Найти нули функции 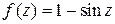и определить их порядок.

Решение. Из уравнения 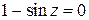находим нули заданной функции:

.

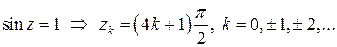Вычисляем производные функции и находим их значения в точках :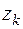

,

.

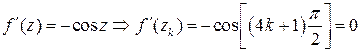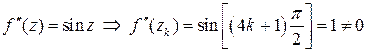Получили 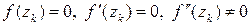. Значит, точки 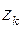– нули 2-го порядка заданной функции. ☻

Задача 6. Найти нули функции 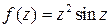и определить их порядок.

Ответ. Точка 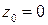– 3-кратный нуль, нули 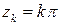, 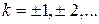– простые.

Пример 7. Найти порядок нуля 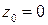функции .

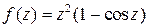Решение. Вспомним разложение функции 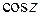в ряд по степеням :

.

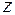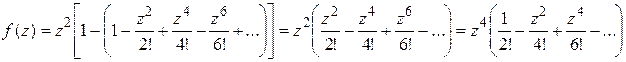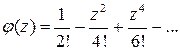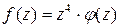Положим , тогда функция представится в виде , где 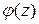– аналитическая в точке 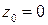функция (ибо она представлена степенным рядом, сходящимся в круге 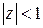), причем 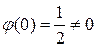. В силу (6) точка 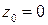– это нуль 4 –го порядка данной функции. ☻

Задача 7. Показать, что функция 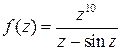в точке 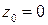имеет нуль 7-го порядка.

Пример 8. Найти порядок всех нулей функции .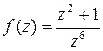

Решение. Легко видеть, что функция имеет нули в точках 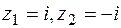, а также в бесконечно удаленной точке 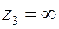. Представим функцию 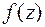в виде

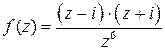
и рассмотрим ее поведение в каждой из трех точек.

1. Точка 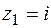. Положим 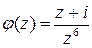– это аналитическая в точке 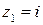функция, причем 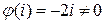. Значит, можем записать 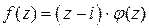. В силу представления (6) точка 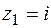является простым нулем данной функции.

2. Точка 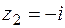. Положим 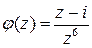– это аналитическая в точке 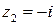функция, причем 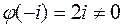. Теперь 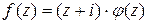, а это значит, что точка 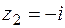также является простым нулем.

3. Точка 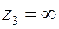. Положим 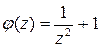– это аналитическая на всей плоскости функция, 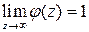. Теперь 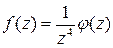и в силу представления (7) точка 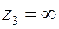является нулем 4–го порядка данной функции. ☻