2015-03-27
573
Существуют случайные величины множество значений которой, может быть произвольным: множество всех действительных чисел, полупрямая [а; +¥), отрезок [a; b] и т.п. Такие случайные величины, в отличие о дискретных, не могут быть заданы законом распределения. Для любой случайной величины X можно вести понятие функции распределения F(х).
Значение функции распределения F(х) в точке х определяется как вероятность того, что в результате испытания случайная величина Х примет значение, меньшее, чем х:
F(x)=P(X<x).
Примеры нахождения функций распределения.
Задача 1. Пусть Х – ДСВ с законом распределения:
| Х | 1 | 2 | 3 |
| Р | 0,2 | 0,5 | 0,3 |
Решение. Разобьем всю прямую на четыре части точками х1=1, х2=2, х3=3, а затем рассмотрим четыре случая:
- если х£1, то событие {Х<x} является невозможным, поэтому F(x)=P(0)=0;
- если 1<x£2, то событие {X<x} возможно лишь тогда, когда Х=1, поэтому F(x)=P(X<x)=P(X=1)=0/2;
- если 2<x£3, то событие {X<x} возможно тогда, когда Х=1 или Х=2, поэтому по формуле сложения вероятностей F(x)=P(X<x)=P(X=1)+P(X=2)=0.7;
|
|
|
- наконец, если x³3, то событие {X<x} является достоверным, поэтому F(x)=P(X<x)=P(W)=1.
Таким образом, функция распределения этой случайной величины имеет вид:
y y=F(x)
0, если х£1 1
F(x)= 0,2, если 1<х£2
0,7, если 2<х£3 0.7
1, если х>3
0.2
x
1 2 3
Функции такого вида называют ступенчатыми.
Задача 2. Рассмотрим испытание, состоящее в том, что в заданном круге радиуса R=1 наугад отмечается точка М. Пусть случайная величина Х – это расстояние от точки М до центра круга.
Решение. Рассмотрим три случая:
- если x£0, то событие {X<x} является невозможным, т.к. расстояние Х не может быть отрицательным, а поэтому F(x)=P(X<x)=p=0;
- если же x>1, то событие {X<x}, напротив, является достоверным, поэтому F(x)=P(X<x)=p(W)=1;
- наконец, если 0<x£1, то событие {X<x} означает попадание т. М внутрь круга радиуса х с тем же центром, поэтому:
F(x)=P(X<x)=px2/pR2=x2
(см. геометрическое определение вероятности).
Таким образом, эта случайная величина Х имеет следующую функцию распределения:
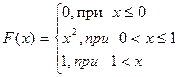y
1
1
Отметим, что в рассмотренном примере, в отличие от предыдущего, функция распределения F(x) оказалась непрерывной.
Случайная величина Х называется непрерывной, если ее функция распределения F(x) удовлетворяет двум условиям:
1.F(x) – непрерывна на всей числовой прямой;
2.F(x) – кусочно-дифференцируема.
Отметим простейшие свойства функции распределения:
1.F(x) – монотонно неубывающая функция;
2. 
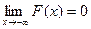
3. 
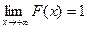
В то же время верно и обратное, т.е. любую функцию F(x), которая является непрерывной, кусочно-дифференцируемой, а также удовлетворяет указанным выше свойствам 1-3, можно рассматривать как функцию распределения некоторой НСВ Х.
|
|
|
Другим, важным понятием, связанным с НСВ Х, является понятие плотности распределения: она обозначается через f(x) и определяется как производная от функции распределения, т.е.
f(x)=F¢(x).
Так, например, в рассмотренной выше задаче с бросанием точки в круг плотность распределения f(x) имеет вид.
y
2
0, если х£0
f(x)= 2x, если 0<х£1
0, если х³1
1 x
Плотность f(x) не обязательно должна быть непрерывной на всей прямой – в некоторых точках она может иметь разрывы.
В некоторых задачах НСВ Х задается своей плотностью распределения f(x). В таком случае функция распределения F(x) может быть найдена по формуле:
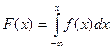
Основные свойства плотности распределения:
1) 
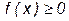для любого x,
2) 
.
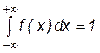3) Функция распределения F(x) может быть найдена по формуле:
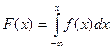
4) Вероятность попадания НСВ Х в заданный интервал (a, b) можно найти по одной из следующих формул:
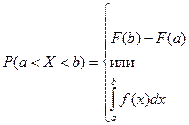
5) Из теоремы о среднем определенного интеграла, при a=x и b=x+Dx получаем приближенную формулу:
P(x<X<x+Dx)»f(x)× Dx.
Эта формула выражает вероятностный смысл плотности распределения: если всю числовую прямую разбить на достаточно маленькие интервалы одинаковой длины Dх, то вероятность попадания Х в каждый из этих интервалов пропорциональна значению f(x) на этом интервале. Что соответствует физическому понятию плотности тела.
