В элементарной геометрии измерялись длины прямолинейных отрезков, а также длина окружности и ее частей. За длину окружности принимается предел периметров правильных вписанных в окружность многоугольников при неограниченном увеличении числа их сторон. Обобщим это понятие для любой кривой.
Определение. Длиной L дуги АВ называется предел, к которому стремится периметр вписанной в эту дугу ломанной, когда число ее звеньев неограниченно растет, а наибольшая из длин звеньев стремится к нулю:
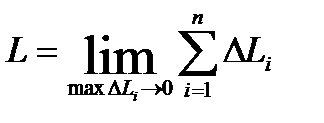
Кривые, для которых этот предел существует, называются спрямляемыми.
Теорема. Пусть кривая АВ задана уравнением y=f(x), где f(x) – непрерывная функция, имеющая непрерывную производную во всех точках сегмента [ a;b ]. Тогда дуга АВ имеет длину:
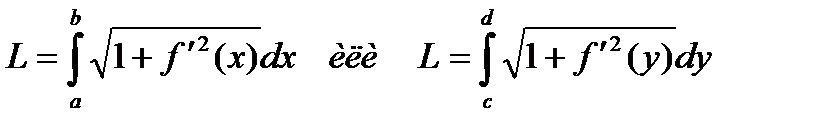 ,
,
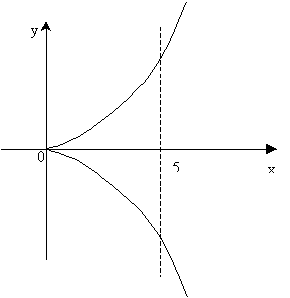 | Пример 1.Найти длину дуги полукубической параболы 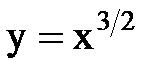 от х=0 до х=5. Решение:Кривая симметрична относительно оси Ох. Найдем длину верхней ветви кривой. Из уравнения от х=0 до х=5. Решение:Кривая симметрична относительно оси Ох. Найдем длину верхней ветви кривой. Из уравнения 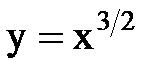 находим находим 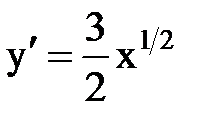 . Далее, применяя формулу, получим . Далее, применяя формулу, получим 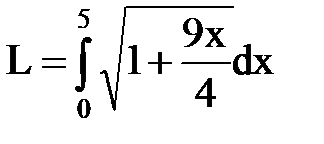 = = 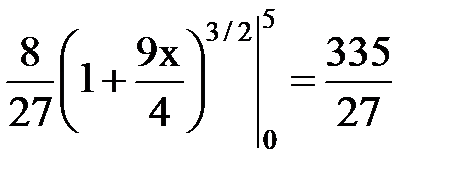 (ед.) (ед.) |
Пример 2. Вычислить длину дуги параболы у2=4х от х=0 до х=1.
Решение.
| у |
| х |
| -2 |
Для нахождения длины дуги параболы можно воспользоваться формулами: 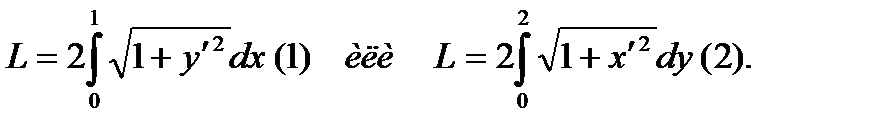 Так как Так как 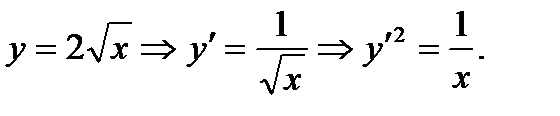 Тогда по формуле (1) получим: Тогда по формуле (1) получим: 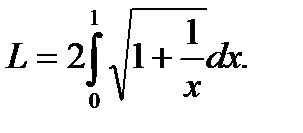 Этот интеграл довольно сложный. Поэтому воспользуемся формулой (2) Этот интеграл довольно сложный. Поэтому воспользуемся формулой (2) |
Для этого выразим из уравнения параболы х и найдем производную по «игреку»:
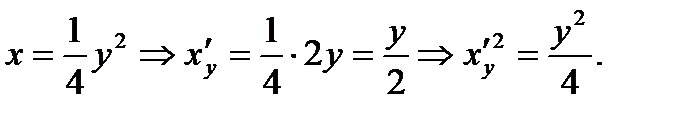
Тогда длина дуги будет равна:
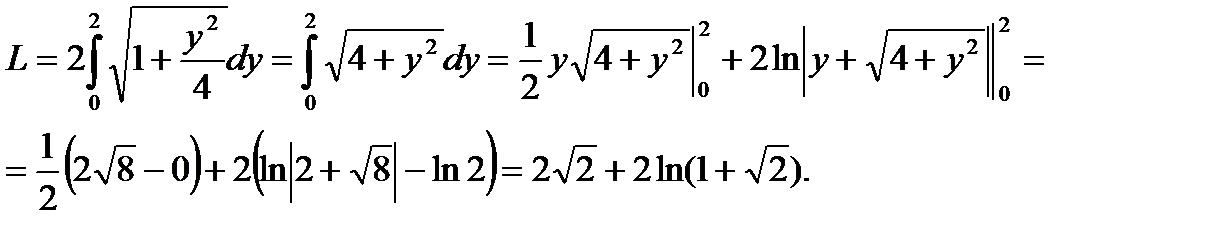
Замечание. 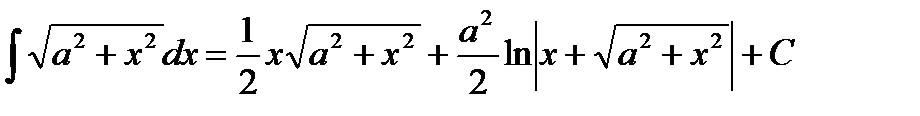
 2015-03-07
2015-03-07 6565
6565








