а) Вычислить определенный интеграл 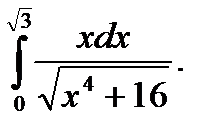
Решение.
Главный вопрос здесь вовсе не в определенном интеграле, а в том, как правильно провести замену. Смотрим в таблицу интегралов и прикидываем, на что у нас больше всего похожа подынтегральная функция? Очевидно, что на длинный логарифм: 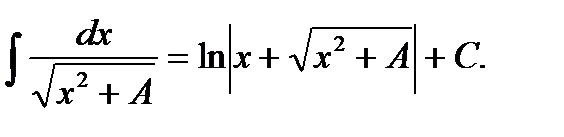 . Но в табличном интеграле под корнем x2, а в нашем – «икс» в четвёртой степени. Поэтому совершенно естественно напрашивается замена: t=x2
. Но в табличном интеграле под корнем x2, а в нашем – «икс» в четвёртой степени. Поэтому совершенно естественно напрашивается замена: t=x2
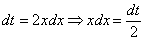
Находим новые пределы интегрирования.
Сначала подставляем в выражение замены t=x2 нижний предел интегрирования, то есть, ноль:
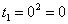
Потом подставляем в выражение замены t=x2 верхний предел интегрирования, то есть, корень из трёх:
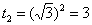
Продолжаем решение.

(1) В соответствии с заменой записываем новый интеграл с новыми пределами интегрирования.
(2) Это простейший табличный интеграл, интегрируем по таблице.
(3) Используем формулу Ньютона-Лейбница 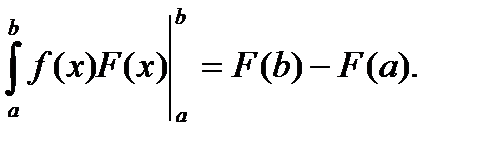
Ещё одно отличие от неопределенного интеграла состоит в том, что, после того, как мы провели замену, никаких обратных замен проводить не надо.
b) Найти определенный интеграл методом замены переменной 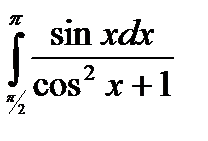
Решение.
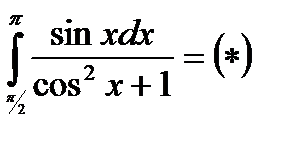
Проведем замену переменной: 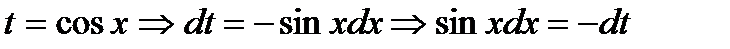
Новые переделы интегрирования:
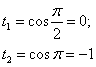
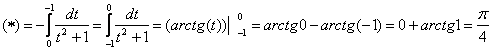
c) Найти определенный интеграл методом замены переменной 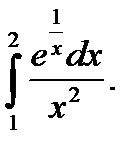
Решение.
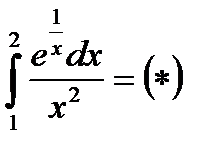
Проведем замену переменно: 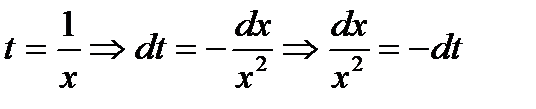
Новые пределы интегрирования:
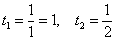
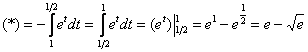
 2015-03-07
2015-03-07 3396
3396
