1.Вычислить неопределенные интегралы.
| Вариант | а) Вычислить интегралы методом непосредственного интегрирования: | б) Вычислите интегралы методом замены переменной или подведением под знак дифференциала. | в) Вычислите интеграл методом интегрирования по частям. |
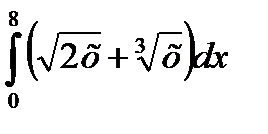
| 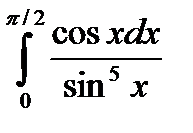
| 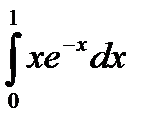
| |
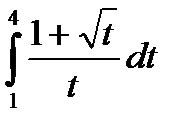
| 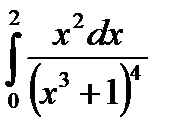
| 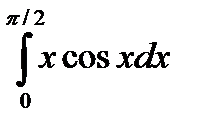
| |
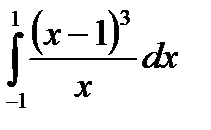
| 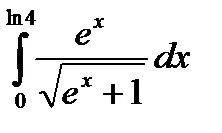
| 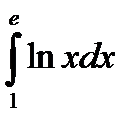
| |
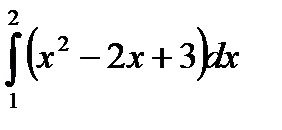
| 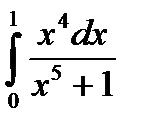
| 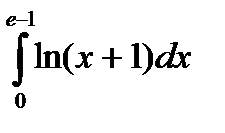
| |
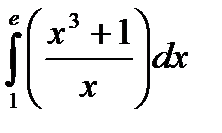
| 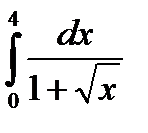
| 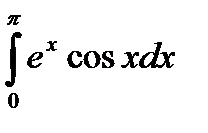
| |
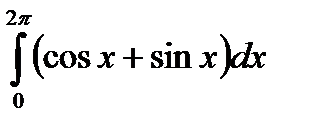
| 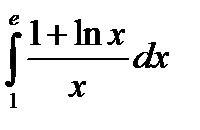
| 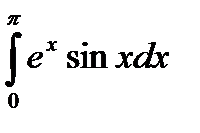
| |
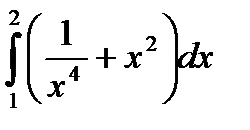
| 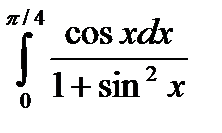
| 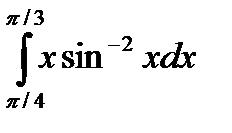
| |
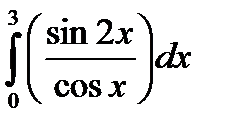
| 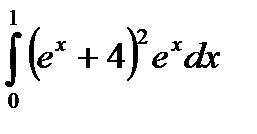
| 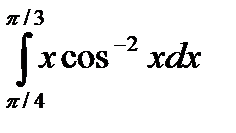
| |
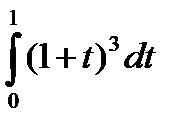
| 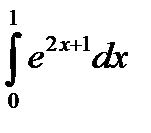
| 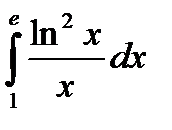
| |
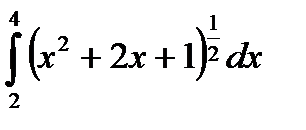
| 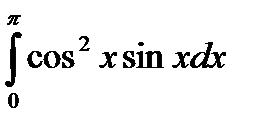
| 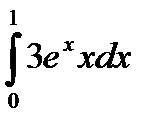
| |
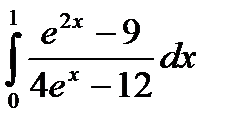
| 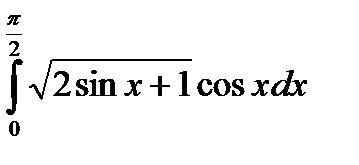
| 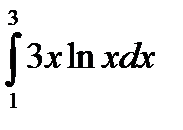
| |
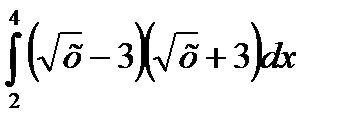
| 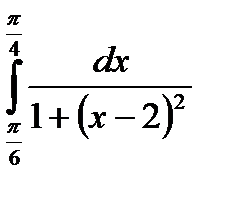
| 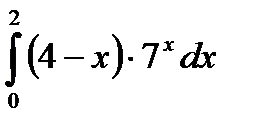
| |
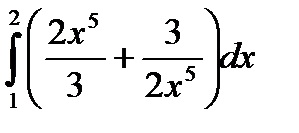
| 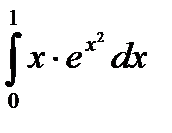
| 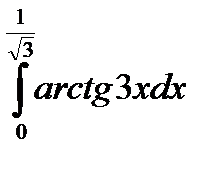
| |
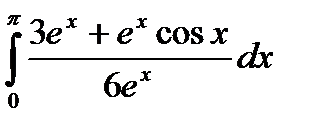
| 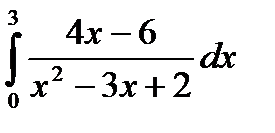
| 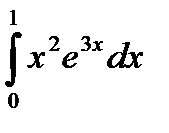
| |
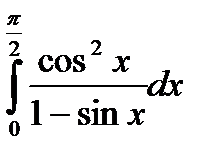
| 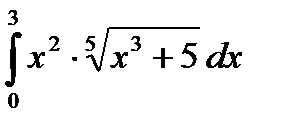
| 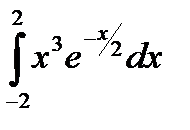
| |
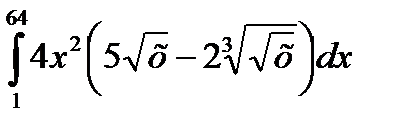
| 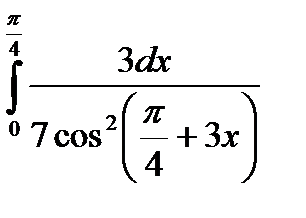
| 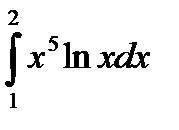
| |
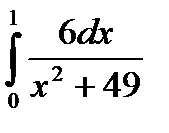
| 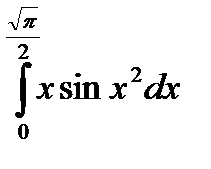
| 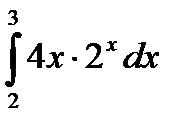
| |
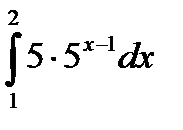
| 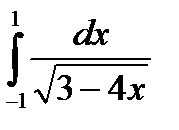
| 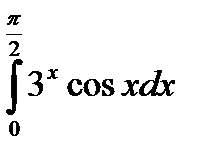
| |
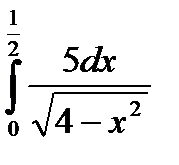
| 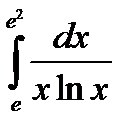
| 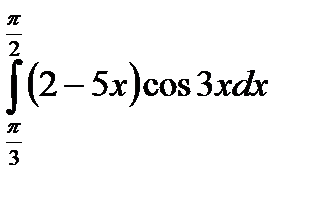
| |
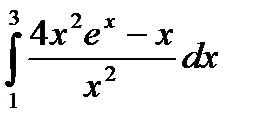
| 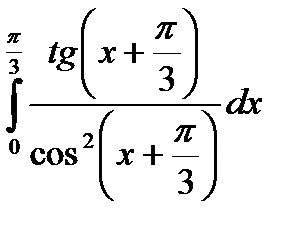
| 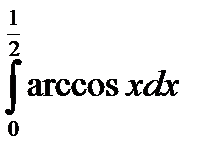
| |
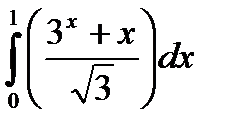
| 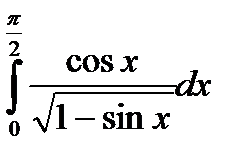
| 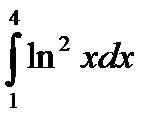
| |
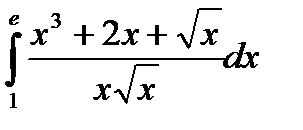
| 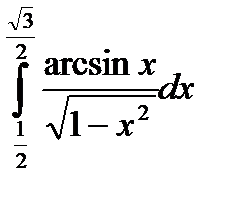
| 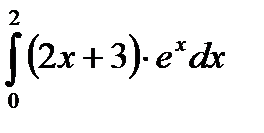
| |
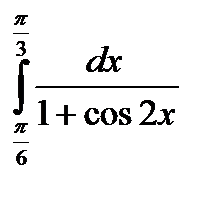
| 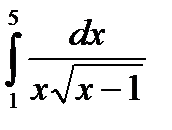
| 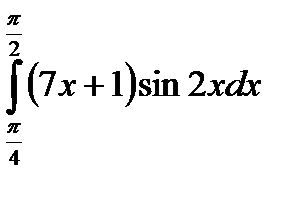
| |
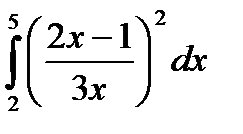
| 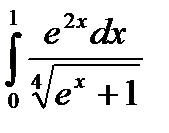
| 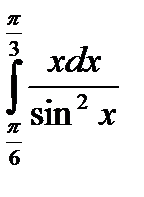
|
2. Предварительно выполнив чертеж, найти площадь фигур, ограниченных линиями.
| Вариант | Уравнения линий |
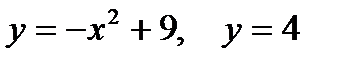
| |
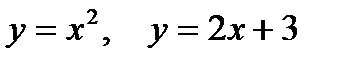
| |
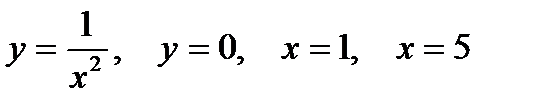
| |
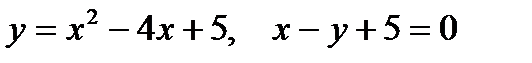
| |
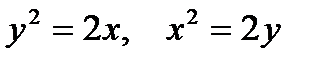
| |
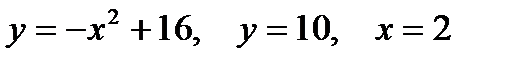
| |
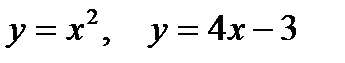
| |
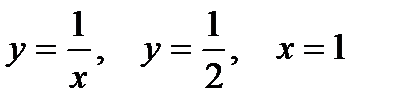
| |
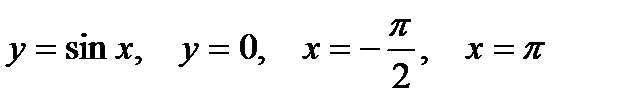
| |
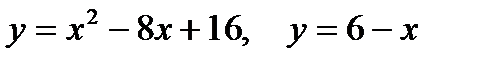
| |
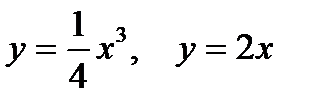
| |
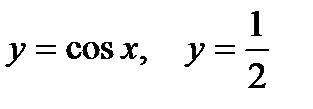
| |
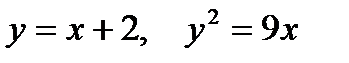
| |
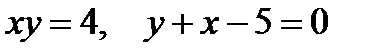
| |
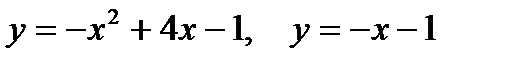
| |
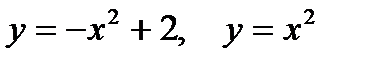
| |
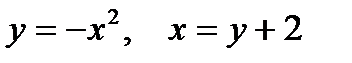
| |
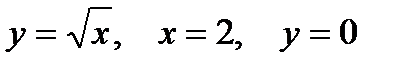
| |
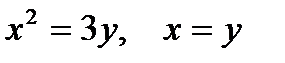
| |
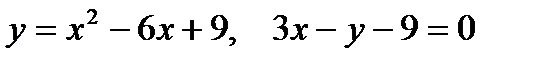
| |
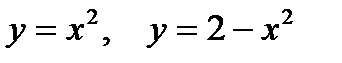
| |
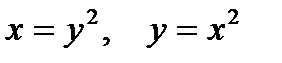
| |
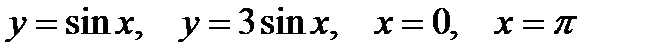
| |
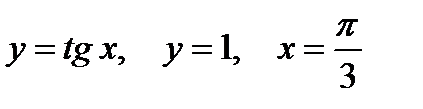
|
3. Определить объем тела, образованного вращением вокруг координатной оси (для четных вариантов – вокруг оси Ох, для нечетных вариантов – вокруг оси Oy), ограниченного линиями:
| Вариант | Уравнения линий |
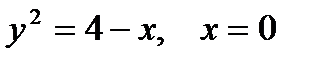
| |
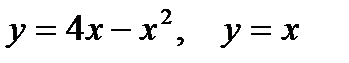
| |
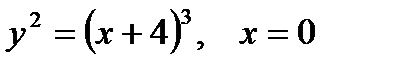
| |
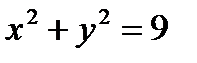
| |
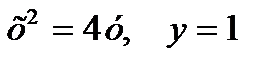
| |
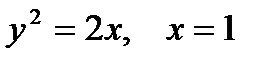
| |
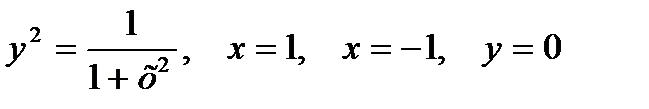
| |
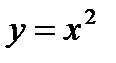 , , 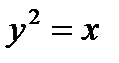
| |
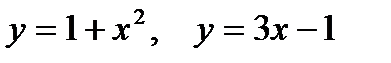
| |
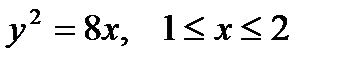
| |
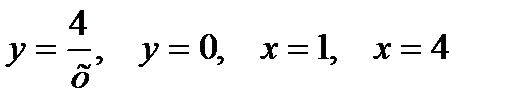
| |
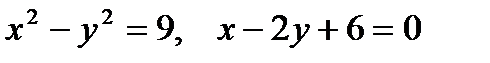
| |
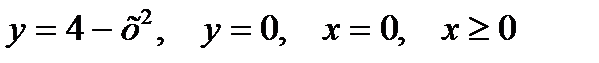
| |
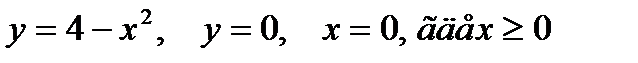
| |
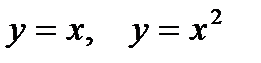
| |
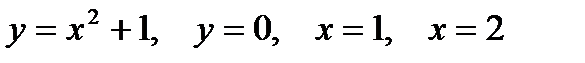
| |
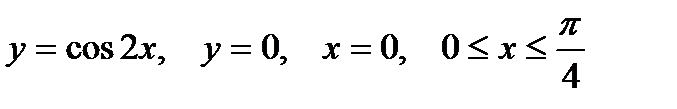
| |
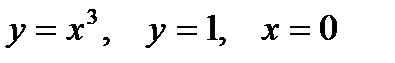
| |
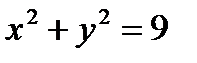
| |
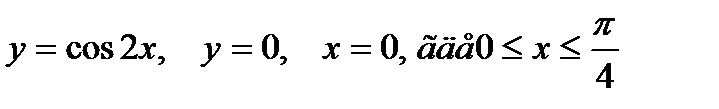
| |
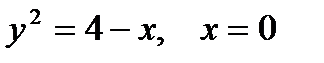
| |
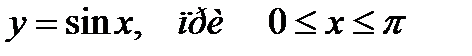
| |
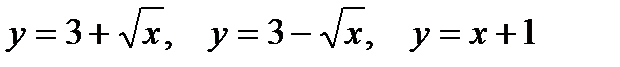
| |
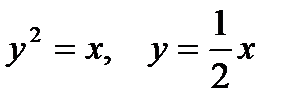
|
|
|
|
 2015-03-07
2015-03-07 589
589







