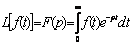 (2.3)
(2.3)
Отметим, что функцию действительной переменной f(t) называют оригиналом, а функцию комплексной переменной p F(p) называют изображением по Лапласу.
В соответствии с формулой (2.3) оригинал
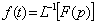 .
.
Среди свойств преобразования Лапласа выделим свойство:
Если справедливо преобразование (2.3), то справедливо преобразование
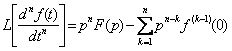 .
.  (2.4)
(2.4)
Запишем формулу (2.4) для случаев n=1 и n=2 (изображение по Лапласу для первой и второй производных).
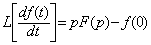 ,
,
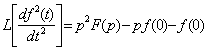 ,
,
т.е. при ненулевых начальных условиях необходимо учитывать начальные условия оригинала и (n-1) его производных.
При нулевых начальных условиях (рассматривается вынужденное движение)
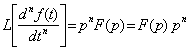 . (2.5)
. (2.5)
Выражение (2.5) показывает, что применение преобразования Лапласа к обеим частям дифференциального уравнения позволяет “алгебраизировать” это уравнение, что упрощает исследование линейных звеньев и систем.
Применив преобразование Лапласа при нулевых начальных условиях к обеим частям дифференциального уравнения (2.1), получим уравнение в изображениях
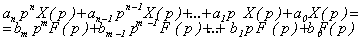 , (2.6)
, (2.6)
которое можно переписать в форме
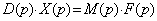 , (2.7)
, (2.7)
где
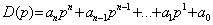 - (2.8)
- (2.8)
собственный оператор линейного звена или системы,
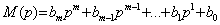 - (2.9)
- (2.9)
взаимный оператор линейного звена или системы.
Обратим внимание на то, что уравнение
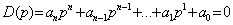 (2.10)
(2.10)
есть характеристическое уравнение линейного дифференциального уравнения (2.1). Напомним, что корни этого уравнения определяют частоты свободных колебаний линейной динамической системы или звена.
Взаимный оператор определяет преобразование входного воздействия.
Передаточной функцией линейного звена или системы называется отношение изображений по Лапласу выходной и входной переменных (при нулевых начальных условиях).
Из уравнений в изображениях (2.6) и (2.7) можно записать аналитическое выражение для передаточной функции
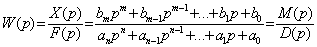 . (2.11)
. (2.11)
Передаточная функция является важнейшей динамической характеристикой линейной системы или звена, так как, зная передаточную функцию и изображение по Лапласу входного сигнала, можно найти изображение по Лапласу выходной величины. Действительно, из (2.11) следует, что
X(p) = W(p)·F(p). (2.12)
Напомним, что имеются таблицы соответствий оригиналов и их изображений по Лапласу.
Основные свойства передаточной функции:
1) Во всякой физически реализуемой системе (звене) степень (m) полинома числителя передаточной функции не больше степени (n) полинома ее знаменателя, т.е.
m £ n. (2.13)
Это обусловлено тем, что в природе не существует идеальных дифференцирующих устройств. Поэтому в реальных звеньях и системах реакция на выходе наступает после или в момент приложения воздействия, т.е. при t³0.
2) Знаменатель передаточной функции D(p) - собственный оператор системы (звена) или характеристический многочлен, а его нули есть корни характеристического уравнения (2.8). В математике их принято называть полюсами передаточной функции, так как при комплексной переменной p, равной любому полюсу, W(p) обращается в бесконечность. Корни уравнения M(p)=0 называют нулями передаточной функции т.к. при комплексной переменной р, равной любому нулю, числитель W(p) обращается в нуль.
3) При p=0 (см. (2.11))
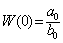 =К (2.14)
=К (2.14)
есть передаточный коэффициент системы или звена.
Стандартная форма записи передаточной функции имеет вид
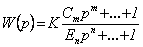 ,
,
когда в полиномах числителя и знаменателя свободный член равен 1.
4) Свободное движение линейной системы или звена определяется полюсами передаточной функции. Действительно, для нахождения свободного движения в дифференциальном уравнении (2.1) следует положить f(t)=0. В результате получаем
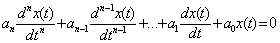 .
.
Общее решение этого однородного дифференциального уравнения имеет вид
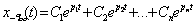 , (2.15)
, (2.15)
где 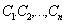 - произвольные постоянные, определяемые начальными условиями,
- произвольные постоянные, определяемые начальными условиями,
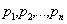 - корни характеристического уравнения (2.10).
- корни характеристического уравнения (2.10).
 2015-03-27
2015-03-27 1267
1267
