Запасы устойчивости

Анализ устойчивости по логарифмическим характеристикам ЛЧХ разомкнутых систем выполняется на основе критерия устойчивости Найквиста-Михайлова.

АФХ разомкнутых систем в зависимости от пересечения с вещественной осью относительно критической точки с координатами (- 1, j0) можно подразделить на два типа: первый, когда все точки пересечения АФХ с вещественной осью расположены справа от критической точки (рис. 4.5); второй, когда точки пересечения АФХ с вещественной осью расположены справа и слева от критической точки (рис. 4.4).

Рассмотрим взаимнооднозначное соответствие между АФХ первого типа и ЛЧХ.

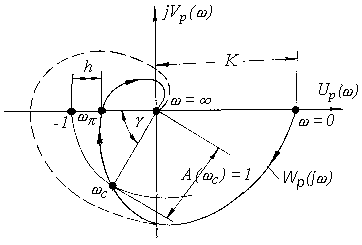
Рис. 4.5. АФХ первого типа

АФХ первого типа, показанная на рис 4.5 сплошной линией, соответствует системе, устойчивой в замкнутом состоянии. На этой АФХ выделены две частоты: частота среза (wс), при которой çWp(jwс)ç=А(wс)=1 и частота wp, при которой arg Wp(jwp)=jp(wp)=-180°.

Для устойчивых замкнутых систем удаление годографа Wp(jw) от критической точки (- 1, j 0) характеризуется запасами устойчивости по фазе и модулю. Минимальный угол g, образуемый вектором W p (jw с ) и отрицательной частью действительной оси, называетсязапасом устойчивости по фазе

Минимальный отрезок действительной оси h, характеризующий расстояние между критической и ближайшей точкой пересечения годографом W p (jw) с действительной осью называют запасом устойчивости по модулю.

Отобразим рис. 4.5 на плоскость ЛЧХ (рис. 4.6).

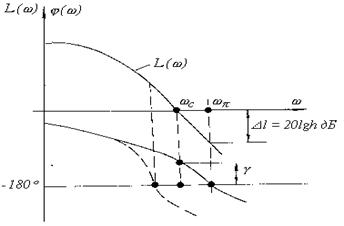
Рис. 4.6. Логарифмические частотные характеристики разомкнутой системы, соответствующие устойчивой замкнутой системе (сплошные линии) и неустойчивой замкнутой системе (пунктирная линия)

Рассмотренное позволяет сделать вывод:

система, устойчивая в разомкнутом состоянии и имеющая АФХ первого типа, устойчива в замкнутом состоянии, если при всех частотах, при которых ЛАЧХ положительна, т.е. L(w)³ 0,j(w)>-180°.