В некоторых учебниках и учебных пособиях этот критерий именуется критерием Найквиста - Михайлова. Это объясняется тем, что этот критерий был предложен американским ученым Х. Найквистом для анализа устойчивости усилителей с обратной связью. Позднее А.В. Михайлов доказал возможность его применения для анализа устойчивости линейных САУ.
Основная особенность и практическая ценность этого критерия заключается в том, что анализ устойчивости замкнутой системы выполняется по частотным характеристикам разомкнутого контура регулирования.
Рассматриваются три случая анализа устойчивости: 1) система в разомкнутом состоянии устойчива; 2) система в разомкнутом состоянии неустойчива; 3) система в разомкнутом состоянии нейтрально устойчива (нулевые корни в характеристическом уравнении разомкнутой системы, что возможно при наличии в контуре регулирования интегрирующих звеньев).
Рассмотрим анализ устойчивости замкнутой системы для случая, когда эта система устойчива в разомкнутом состоянии. Для этого случая дадим физическое объяснение и доказательство. Поэтому уместно поставить вопрос: почему система, устойчивая в разомкнутом состоянии, может оказаться неустойчивой в замкнутом состоянии?
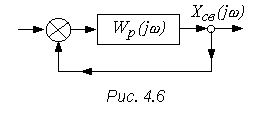
Целесообразно проанализировать преобразование в контуре регулирования отдельных составляющих сигнала на выходе (рис. 4.2)
|
Допустим, на частоте wp argWp(jwp)=-180°. Следовательно, на этой частоте отрицательная обратная связь превращается в положительную.
При этом возможны три варианта:
1) Модуль частотной передаточной функции разомкнутой системы на частоте wp çWp(jwp)ç<1, что ведет к затуханию колебаний сигнала на этой частоте в замкнутом контуре, а это свидетельствует об устойчивости такой системы.
2) çWp(jwp)ç=1, что свидетельствует о возникновении незатухающих колебаний с частотой wp, т.е. замкнутая система находится на колебательной границе устойчивости (частота незатухающих колебаний wp).
3) çWp(jwp)ç>1, что ведет к увеличению амплитуды колебаний на частоте wp и, следовательно, такая система неустойчива.
Отобразим три возможных варианта поведения замкнутой системы на плоскости АФХ разомкнутой системы (см. рис. 4.3).
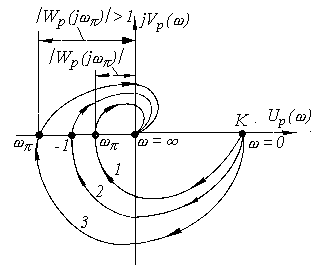
Рис. 4.3. Амплитудно-фазовые характеристики разомкнутой системы для трех вариантов преобразования гармоники Xсв(jw) на частоте wp
Рассмотренная выше физическая трактовка динамических свойств замкнутой системы и рис. 4.3 позволяют сделать заключение о том, что
 если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала точку с координатами (1, j0).
если система устойчива в разомкнутом состоянии, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала точку с координатами (1, j0).
 2015-03-27
2015-03-27 490
490