Найдите область сходимости степенного ряда 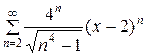
Решение.
Найдем радиус сходимости:
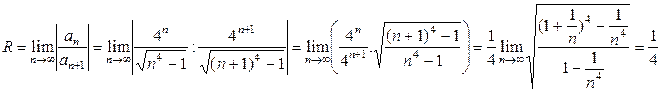 . Следовательно, интервал сходимости:
. Следовательно, интервал сходимости:
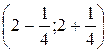 или
или 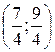 .
.
Исследуем сходимость на концах интервала:
1) 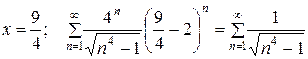 . (1)
. (1)
Для исследования ряда (1) применим предельный признак сравнения с гармоническим рядом 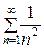 .
.
Проверим выполнение признака:
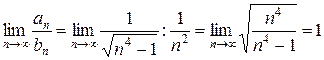 .
.
Так как предел конечный и отличный от нуля, то ряд (1) сходится, так как сходится при s =2> 1 гармонический ряд.
2) 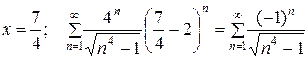 . (2)
. (2)
Применим к исследованию знакочередующегося ряда (2) признак Лейбница.
Так как абсолютные величины ряда (2) монотонно убывают и 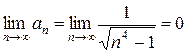 ,
, 
то по признаку сходимости Лейбница данный ряд сходится.
Ответ: область сходимости 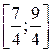 .
.
 2015-03-07
2015-03-07 411
411








