Начальные условия показывают, в каком состоянии находилась струна в момент начала колебаний. Удобнее всего считать, что струна начала колебаться в момент времени 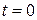 . Начальное положение точек струны задается условием:
. Начальное положение точек струны задается условием:
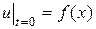 , (2.2)
, (2.2)
а начальная скорость:
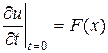 , (2.3)
, (2.3)
где 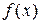 и
и 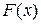 – заданные функции.
– заданные функции.
Записанные начальные условия аналогичны начальным условиям в простейшей задаче динамики материальной точки. Там для определения закона движения материальной точки нужно знать начальное положение точки и ее начальную скорость.
Иной характер имеют краевые условия. Они показывают, что происходит на концах струны во все время колебаний. В простейшем случае, когда концы струны закреплены (начало струны – в начале координат, а конец в точке 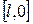 ), функция
), функция 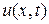 будет подчиняться условиям:
будет подчиняться условиям:
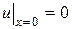 ,
, 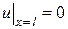 . (2.4)
. (2.4)
Сформулируем окончательную математическую задачу, к которой приводит изучение свободных колебаний струны, закрепленной на обоих концах.
Требуется решить однородное линейное дифференциальное уравнение с частными производными второго порядка с постоянными коэффициентами:
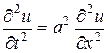 (2.5)
(2.5)
при начальных условиях
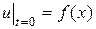 ,
, 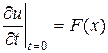 (2.6)
(2.6)
и краевых условиях
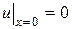 ,
, 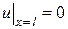 . (2.7)
. (2.7)
Функции 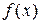 и
и 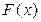 определены на интервале
определены на интервале 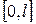 и, как следует из первого начального условия и краевых условий,
и, как следует из первого начального условия и краевых условий, 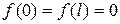 .
.
 2015-03-07
2015-03-07 1319
1319
