Пусть в начальный момент задана температура в различных сечениях неограниченного стержня. Требуется определить распределение температуры в стержне в последующие моменты времени (к задаче распространения тепла в неограниченном стержне сводятся физические задачи в том случае, когда стержень столь длинный, что температура во внутренних точках стержня в рассматриваемые моменты времени мало зависит от условий на концах стержня).
Если стержень совпадает с осью 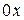 (рис.3.1), то математическая задача формулируется следующим образом. Найти решение уравнения:
(рис.3.1), то математическая задача формулируется следующим образом. Найти решение уравнения:
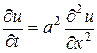 (3.30)
(3.30)
в области 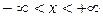 ,
, 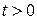 , удовлетворяющее начальному условию:
, удовлетворяющее начальному условию:
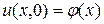 . (3.31)
. (3.31)
Это задача Коши для уравнения теплопроводности.
Применим для нахождения решения метод разделения переменных, т.е. будем искать частное решение уравнения (3.30) в виде произведения двух функций:
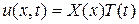 . (3.32)
. (3.32)
Подставляя в уравнение (3.30), будем иметь:
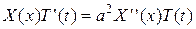
или:
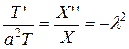 . (3.33)
. (3.33)
Каждое из этих отношений не может зависеть ни от 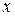 , ни от
, ни от 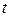 , и потому их приравниваем к постоянной
, и потому их приравниваем к постоянной 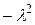 . Из (3.33) получаем два уравнения:
. Из (3.33) получаем два уравнения:
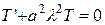 , (3.34)
, (3.34)
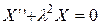 . (3.35)
. (3.35)
Решая их, найдем 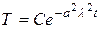 ,
, 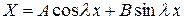 .
.
Подставляя в (3.32) получаем:
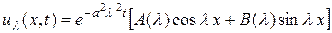 , (3.36)
, (3.36)
где постоянная 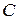 включена в
включена в 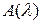 и
и 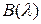 .
.
Для каждого значения 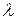 получаем решение вида (3.36). Произвольные постоянные
получаем решение вида (3.36). Произвольные постоянные 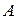 и
и 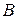 для каждого значения
для каждого значения 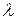 имеют определенные значения. Поэтому можно считать
имеют определенные значения. Поэтому можно считать 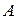 и
и 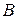 функциями
функциями 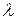 . В силу линейности уравнения (3.30) решением является также сумма решений вида (3.36):
. В силу линейности уравнения (3.30) решением является также сумма решений вида (3.36):
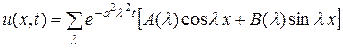 . (3.37)
. (3.37)
Интегрируя выражение (3.36) по параметру 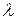 в пределах от
в пределах от 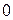 до
до 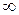 , также получим решение:
, также получим решение:
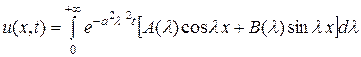 , (3.38)
, (3.38)
если 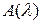 и
и 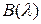 таковы, что этот интеграл, его производная по
таковы, что этот интеграл, его производная по 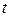 и вторая производная по
и вторая производная по 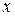 существуют и получаются путем дифференцирования интеграла по
существуют и получаются путем дифференцирования интеграла по 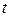 и
и 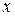 . Подберем
. Подберем 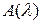 и
и 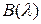 так, чтобы решение
так, чтобы решение 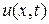 удовлетворяло условию (3.31). Полагая в равенстве (3.38)
удовлетворяло условию (3.31). Полагая в равенстве (3.38) 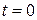 , на основании условия (3.31) получаем:
, на основании условия (3.31) получаем:
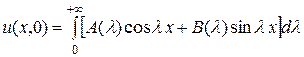 . (3.39)
. (3.39)
Предположим, что функция 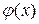 такова, что она представима интегралом Фурье:
такова, что она представима интегралом Фурье: 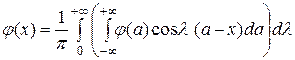 или
или
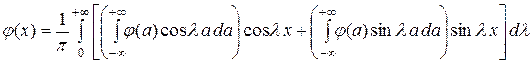 . (3.40)
. (3.40)
Сравнивая правые части (3.39) и (3.40), получаем:
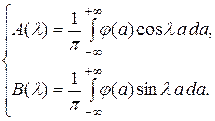 (3.41)
(3.41)
Подставляя найденные выражения 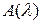 и
и 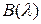 в формулу (3.38), получим:
в формулу (3.38), получим:
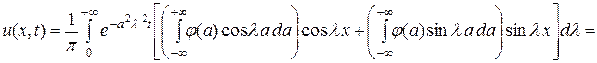
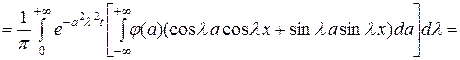
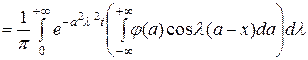
или, переставляя порядок интегрирования, окончательно получим:
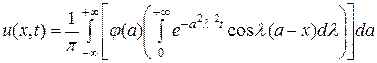 . (3.42)
. (3.42)
Это и есть решение поставленной задачи.
Преобразуем формулу (3.42). Вычислим интеграл, стоящий в круглых скобках:
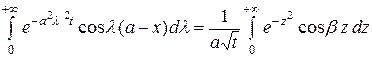 . (3.43)
. (3.43)
Это преобразование интеграла сделано путем подстановок:
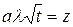 ,
, 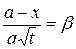 . (3.44)
. (3.44)
Обозначим:
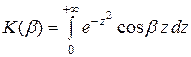 . (3.45)
. (3.45)
Дифференцируя, получаем: 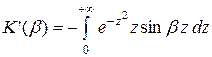 .
.
Интегрируя по частям, найдем:
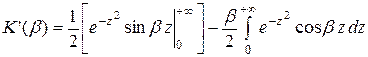
или 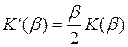 .
.
Интегрируя это дифференциальное уравнение, получим:
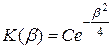 . (3.46)
. (3.46)
Определим постоянную 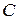 . Из (3.45) следует:
. Из (3.45) следует: 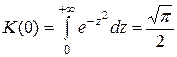 (т.к.
(т.к. 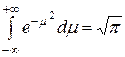 ). Следовательно, в равенстве (3.46) должно быть
). Следовательно, в равенстве (3.46) должно быть 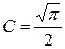 .
.
Итак,
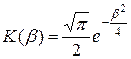 . (3.47)
. (3.47)
Значение (3.47) интеграла (3.45) подставляем в (3.43):
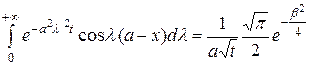 .
.
Подставляя вместо 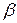 его выражение (3.44), окончательно получаем значение интеграла (3.43):
его выражение (3.44), окончательно получаем значение интеграла (3.43):
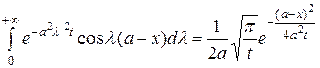 . (3.48)
. (3.48)
Подставив это выражение интеграла в решение (3.42), окончательно получим:
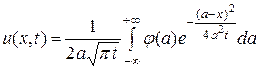 . (3.49)
. (3.49)
Эта формула, называемая интегралом Пуассона, представляет собой решение поставленной задачи о распространении тепла в неограниченном стержне.
Установим физический смысл формулы (3.49). Рассмотрим функцию:
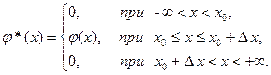 (3.50)
(3.50)
Тогда функция:
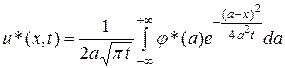 (3.51)
(3.51)
есть решение уравнения (3.30), принимающее при 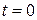 значение
значение 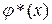 . Принимая во внимание (3.50), можем написать:
. Принимая во внимание (3.50), можем написать:
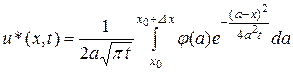 .
.
Применив теорему о среднем к последнему интегралу, получим:
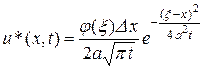 ,
, 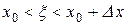 . (3.52)
. (3.52)
Формула (3.52) дает значение температуры в точке стержня в любой момент времени, если при 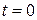 всюду в стержне температура
всюду в стержне температура 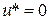 , кроме отрезка
, кроме отрезка 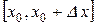 , где она равна
, где она равна 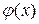 . Сумма температур вида (3.52) и дает решение (3.49). Заметим, что если
. Сумма температур вида (3.52) и дает решение (3.49). Заметим, что если 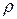 – линейная плотность стержня;
– линейная плотность стержня; 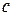 – теплоемкость материала, то количество тепла в элементе
– теплоемкость материала, то количество тепла в элементе 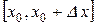 при
при 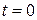 будет:
будет:
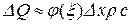 . (3.53)
. (3.53)
Рассмотрим далее функцию:
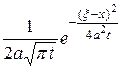 . (3.54)
. (3.54)
Сравнивая ее с правой частью формулы (3.52) с учетом (3.53), говорят, что она дает значение температуры в любой точке стержня в любой момент времени 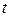 , если при
, если при 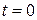 в сечении
в сечении 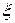 (предельный случай при
(предельный случай при 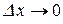 ) был мгновенный источник тепла с количеством тепла
) был мгновенный источник тепла с количеством тепла 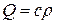 .
.
 2015-03-07
2015-03-07 2002
2002








