2015-03-07
4759
Задача состоит в отыскании решения уравнения теплопроводности:
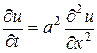(3.61)
при граничных условиях:
, 
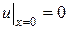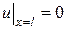(3.62)
и при начальном условии:
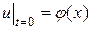, (3.63)
где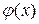 
– непрерывная, имеющая кусочно-непрерывную производную, обращается в нуль пр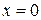и 
и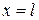 
.
Согласно методу Фурье будем искать нетривиальные решения уравнения (3.61), удовлетворяющие граничным условиям (3.62) в виде:
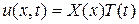. (3.64)
Подставляя (3.64) в (3.61), имеем:
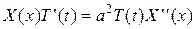
или
,
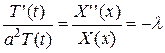откуда получаем два уравнения:
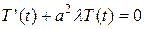, (3.65)
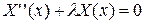. (3.66)
Чтобы получить нетривиальное решение уравнения (3.61) вида (3.64), удовлетворяющее граничным условиям (3.62), необходимо найти нетривиальное решение уравнения (3.66), удовлетворяющее граничным условиям:
, 
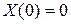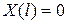. (3.67)
Таким образом, для определения функций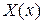 
приходим к задаче о собственных значениях: найти решения линейного дифференциального уравнения второго порядка с заданными граничными условиями:
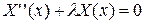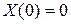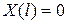, , . (3.68)
Эта задача является частным случаем общей задачи Штурма-Лиувилля, заключающейся в отыскании решений линейного дифференциального уравнения второго порядка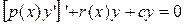 
, удовлетворяющих некоторым краевым условиям, т.е. условиям, налагаемым на искомую функцию или ее производную в точках 
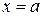и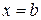 
(концах интервала).
Нетривиальные решения задачи (3.68) возможны лишь при значениях (см. Приложение №1):
, 
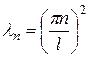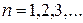(3.69)
Этим собственным числам соответствуют собственные функции:
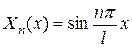. (3.70)
Значениям параметра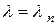 
соответствуют решения уравнения (3.65):
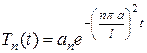, (3.71)
где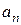 
– произвольные постоянные.
Итак, все функции:
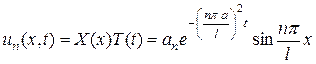(3.72)
удовлетворяют уравнению (3.61) и граничным условиям (3.62) при любых постоянных 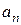. Составим ряд:
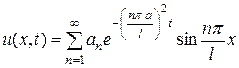. (3.73)
Требуя выполнения начального условия (3.63), получим:
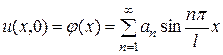. (3.74)
Написанный ряд представляет собой разложение заданной функции 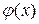в ряд Фурье по синусам в промежутке 
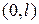. Коэффициенты 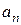разложения определяются по известным формулам:
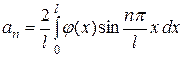. (3.75)
Так как мы предположили, что функция 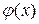непрерывна, имеет кусочно-непрерывную производную и обращается в нуль пр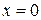и и 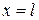, то ряд (3.74) с коэффициентами 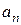, определяемыми по формуле (3.75), равномерно и абсолютно сходится к функции 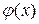. Так как 
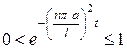при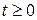 
, то ряд (3.73) при 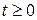также сходится абсолютно и равномерно. Поэтому функция 
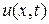, определяемая рядом (3.73), непрерывна в области 
, 
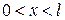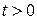и удовлетворяет начальному и граничным условиям.
Остается показать, что функция 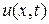удовлетворяет уравнению (3.61) в области 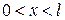, 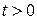. Для этого достаточно показать, что ряды, полученные из (3.73) почленным дифференцированием по 
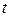один раз и почленным дифференцированием по 
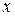два раза, также абсолютно и равномерно сходятся при 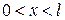, 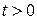. При любом :
, 
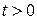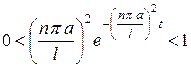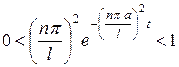
если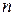 
достаточно велико.
Таким образом, для 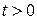задача (3.61) – (3.63) поставлена корректно; напротив, для отрицательных 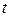задача эта некорректна.
Замечание. В отличие от волнового уравнения:
,
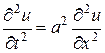уравнение: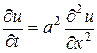
несимметрично относительно времени 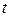: если заменить 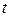на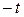 
, то получаем уравнение другого вида:
.
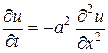Уравнение теплопроводности описывает необратимые процессы: можно предсказать, каким станет данное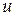 
через промежуток времени длиной 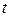, но нельзя с уверенностью сказать, каким было это 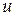за время 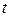до рассматриваемого момента. Это различие между предсказанием и предысторией типично для параболического уравнения и не имеет места, например, для волнового уравнения: в случае последнего заглянуть в прошлое также легко, как и в будущее.
