Распространение тепла в полуограниченном стержне

Рассмотрим задачу о распространении тепла в полуограниченном стержне, боковая поверхность которого теплоизолирована. Пусть конец 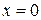поддерживается при заданной температуре, которая может изменяться с течением времени. Тогда задача сводится к решению уравнения:

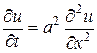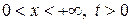, () (3.55)

при граничном условии:

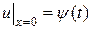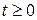, () (3.56)

и начальном условии:

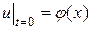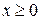, (). (3.57)

Решение задачи (3.55) – (3.57) будем искать в виде суммы:

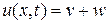, (3.58)

где 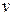и 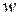– суть решения следующих задач:

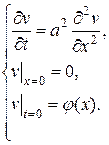(3.59) 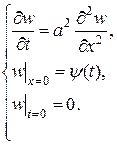(3.60)