2015-03-07
3696
Решить методом Фурье задачу:
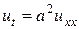(3.100)
при граничных условиях:
, 
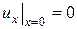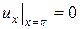(3.101)
и при начальном условии:
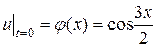. (3.102)
Согласно методу Фурье, ищем частные решения уравнения (3.100) в виде:
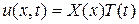. (3.103)
Подставляя (3.103) в (3.100), получим:
,
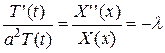откуда получаем два уравнения:
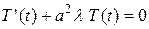, (3.104)
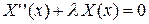. (3.105)
Чтобы получить нетривиальное решение уравнения (3.100) вида (3.103), удовлетворяющее граничным условиям (3.101), необходимо найти нетривиальное решение уравнения (3.105), удовлетворяющее граничным условиям:
, 
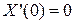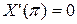. (3.106)
Таким образом, для определения функции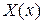 
приходим к задаче о собственных значениях: найти решения линейного дифференциального уравнения второго порядка с заданными граничными условиями:
, , 
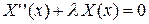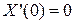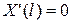. (3.107)
Общее решение этого уравнения будет:
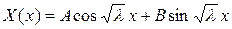, (3.108)
где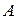 
, 
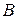– произвольные постоянные.
Найдем производную функции :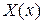
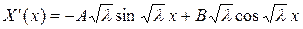. (3.109)
Подставляя значения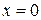 
и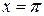 
в равенство (3.109) получаем:
.
.
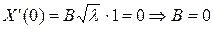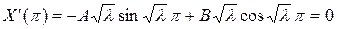Из последнего уравнения следует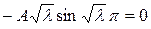 
. 
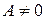, т.к. иначе было бы 
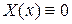и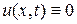 
, что противоречит условию, 
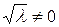, т.к. уравнение теряет смысл. Следовательно, должно быть 
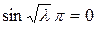, откуда 
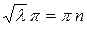. Т.о. получили:
|
|
|
, 
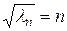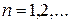(3.110)
Этим собственным числам соответствуют собственные функции:
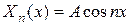. (3.111)
Значениям параметра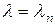 
соответствуют решения уравнения (3.104):
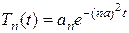, (3.112)
где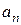 
– произвольные постоянные.
Получили функции:
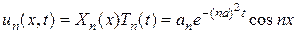, (3.113)
которые удовлетворяют уравнению (3.100) и граничным условиям (3.101) при любых постоянных 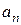. Составим ряд:
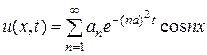. (3.114)
Требуя выполнение начального условия (3.102), получим:
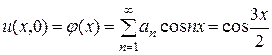. (3.115)
Написанный ряд представляет собой разложение заданной функции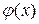 
в ряд Фурье по косинусам в промежутке 
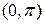. Коэффициенты 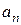определяются по известной формуле:
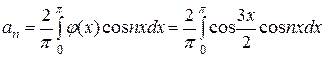. (3.116)
Найденные по выражению (3.116) коэффициентов 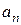подставляются в (3.114) давая решение задачи.
