Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления, то есть:
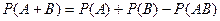 (4.1)
(4.1)
Для несовместных событий их совместное наступление есть невозможное событие Æ, а его вероятность равна нулю. Следовательно, для несовместных событий А, В: 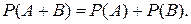 Правило сложения вероятностей справедливо и для конечного числа п попарно несовместных событий, то есть:
Правило сложения вероятностей справедливо и для конечного числа п попарно несовместных событий, то есть:
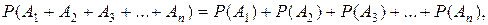 (4.2)
(4.2)
Сумма вероятностей событий 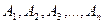 образующих полную группу, равна 1, то есть:
образующих полную группу, равна 1, то есть:
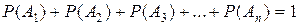 , или
, или 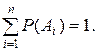 (4.3)
(4.3)
Пример 1. Компания производит 40000 холодильников в год, которые реализуются в различных регионах России. Из них 10000 экспортируются в страны СНГ, 8000 продаются в регионах Европейской части России, 7000 в Дальневосточном районе. Чему равна вероятность того, что определенный холодильник будет а) произведен на экспорт? б) продан в России?
Решение. Обозначим события:
А – «Холодильник будет продан в странах СНГ»,
В – «Холодильник будет продан в Европейской части России»,
С – «Холодильник будет продан в страны дальнего зарубежья»,
D – «Холодильник будет продан в Западной Сибири»,
E – «Холодильник будет продан в Восточной Сибири»,
F – «Холодильник будет продан в Дальневосточном районе».
Соответственно, вероятность того, что холодильник будет продан в странах СНГ: P(A)=10000/40000=0,25. Вероятность того, что холодильник будет продан в Европейской части России: P(B)= 8000/40000=0,20. Вероятность того, что холодильник будет продан в страны дальнего зарубежья: P(C)= 7000/40000=0,175. Вероятность того, что холодильник будет продан в Западной Сибири: P(D)= 6000/40000=0,15. Вероятность того, что холодильник будет продан в Восточной Сибири: P(E)=5000/40000=0,125.
Вероятность того, что холодильник будет продан в Дальневосточном районе:
P(F)= 4000/40000=0,10. События A, B, C, D, E, F – несовместные.
а). Событие, состоящее в том, что холодильник произведен на экспорт,
означает, что холодильник будет продан в страны СНГ, или страны дальнего зарубежья. Отсюда, по формуле (4.2) находим его вероятность P(A+B)=P(A)+P(B)=0,25+0,175=0,425.
б) Событие, состоящее в том, что холодильник будет продан в России, означает, что холодильник будет продан или в Европейской части России, или в Западной Сибири, или в Восточной Сибири, или в Дальневосточном регионе на P(B+D+E+F)= P(b)+P(D)+P(E)+P(F)=0,20+0,15+0,125+0,10=0,575.
Этот же результат можно было получить рассуждая по другому. События «Холодильник произведен на экспорт» и «Холодильник будет продан в России» - два взаимно противоположных события, отсюда по формуле (2.3): Р(холодильник будет продан в России)=1 – Р (холодильник произведен на экспорт)= 1-0,425=0,575.
Ответ: а) 0,425; б) 0,575.
Пример 2. В урне два белых и три черных шара. Чему равна вероятность появления белого а.)шара при первом извлечении из урны? б.)при втором извлечении из урны?
Решение. Здесь возможны два случая.
Первый случай. Схема возвращенного шара, то есть шар после первого испытания возвращается в урну.
Пусть событие А – «появление белого шара при первом испытании». Так как N =5, а М =2, то Р(А) =2/5.
Пусть событие В – «появление белого шара при втором испытании». Так как шар после первого испытания возвращается в урну, то N =5, а М =2 и Р(В) =2/5.
Таким образом, вероятность каждого из событий не зависит от того,
произошло или не произошло другое событие. Событие А и В в этом случае называются независимыми.
Итак, событие А и В называются независимыми, если вероятность каждого из них не зависит от того, произошло или нет другое событие.
Вероятность независимых событий называются безусловными.
Второй случай Схема невозвращенного шара, то есть шар поле первого испытания в урну не возвращается.
Вероятность появления белого шара при первом испытании P(A) =2/5. Белый шар в урну не возвращается, следовательно, в урне остались один белый и три черных шара. Чему равна вероятность события В при условии, что событие А произошло? N=4, M=1.
Искомую вероятность обозначают Р(В/А) или Р(В)А или РА(В). Итак, Р(В/А)=1/4 называют условной вероятностью, а событие А, В называется зависимыми. В предыдущем примере с картами Р(А)=4/52; Р(А/В)=4/16.
Ответ: а.) 0,4; б.) 4/52 и 0,25.
События А и В называются зависимыми, если вероятность каждого из них зависит от того произошло или нет другое событие. Вероятность события В, вычисленная в предположении, что другое событие А уже осуществилось, называется условной вероятностью.
Вероятность произведения двух независимых событий А и В равна произведению их вероятностей: P(AB)= P(A) × P(B) (4.4)
События А1, А2, …, Аn(n>2) называются независимыми в совокупности, если вероятность каждого из них не зависит от того, произошли или нет любые события из числа остальных.
Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятности этих событий.
P(А1 × А2 × …× Аn)= P(А1) × P(А2) ×… × P(Аn) (4.5)
Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого
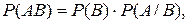
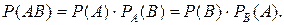 (4.6)
(4.6)
Вероятность совместного наступления конечного числа n зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие уже наступили, то есть
P(А1 × А2 × …× Аn)= P(А1) × P(А2/ А1) × P(А3/ А1× А2) ×… × P(Аn/ А1× А2×…×Аn-1) (4.7)
Если события А1, А2, …, Аn - зависимые в совокупности, то вероятность наступления хотя бы одного из них соответственно равно:
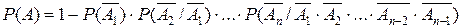 (4.8)
(4.8)
Вероятность появления хотя бы одного события из n независимых в совокупности, равна разности между 1 и произведением вероятности событий, противоположных данным, то есть:
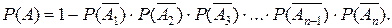 (4.9)
(4.9)
Пример 3. Консультационная фирма претендует на два заказа от двух крупных корпораций. Эксперты фирмы считают, что вероятность получения консультационной работы в корпорации А равна 0,45. Эксперты также полагают, что если фирма получит заказ у корпорации А, то вероятность того, что и корпорация В обратиться к ним, равна 0,9. Какова вероятность того, что консультационная фирма получит оба заказа?
Решение: Обозначим события: А – «получение консультационной работы в корпорации А», В – «получение консультационной работы в корпорации В». События А и В - зависимые, то есть событие В зависит от того, произойдет или нет событие А. По условию мы имеем Р(А)=0,45, а также знаем, что Р(В/А)=0,9. Необходимо найти вероятность того, что оба события (и событие А, и событие В) произойдут, то есть Р(АВ). Для этого используем правило умножения вероятностей: Р(АВ)=Р(А)Р(В/А)=
=0,45 × 0,9 = 0,405.
Ответ: 0,405.
 2015-03-07
2015-03-07 2357
2357
