ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике встречаются опыты, для которых множество таких исходов бесконечно.

Чтобы преодолеть недостаток классического определения вероятности, состоящей в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности - вероятности попадания точки в области.

На плоскости задана квадратируемая область, т.е. область, имеющая площадь. Обозначим эту область буквой G, а ее площадь S_G. В области G содержится область g площади S_g (рис. 1)

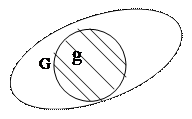Рис. 1

В область G наудачу брошена точка. Будем считать, что брошенная точка может попасть в некоторую часть области G с вероятностью, пропорциональной площади этой части и не зависящей от ее формы и расположения. Пусть A – попадание брошенной точки в области g, тогда геометрическая вероятность этого события определяется формулой

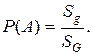(3.1)

Аналогично вводится понятие геометрической вероятности при бросании точки в пространственную область G объема V_G, содержащую область g объема V_g: 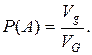(3.2)

В общем случае понятие геометрической вероятности вводится следующим образом. Обозначим меру области (длину, площадь, объем) через mes g, а меру области G – через mes G (mes – первые три буквы французского слова mesure, что значит мера); А- событие «попадание брошенной точки в области g, которая содержится в области G». Вероятность события А будет определяться формулой:

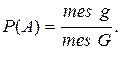(3.3)

Пример 1. В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность того, что точка попадает в квадрат?

Решение. Введем обозначения: R – радиус круга, а - сторона вписанного квадрата, событие А – попадание точки в квадрат, S – площадь круга, S₁ – площадь вписанного квадрата. Как известно, площадь круга S=pR². Сторона вписанного квадрата через радиус описанной окружности выражается формулой 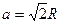, поэтому площадь квадрата S₁= 2R².

По формуле (3.1) S_g=S₁, S_G=S, находим искомую вероятность

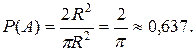
Ответ: 0,637