Числовые характеристики непрерывных случайных величин. Нормальный закон распределени

Функцией распределения случайной величины 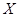называется функция действительной переменной 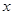, определяемая равенством

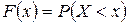, (8.1)

где 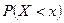- вероятность того, что случайная величина X примет значение, меньшее .

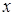Вероятность того, что случайная величина 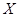примет значение из полуинтервала 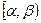, равна разности значений ее функции распределения 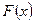на концах этого полуинтервала:

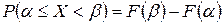. (8.2)

Плотностью распределения вероятностей случайной величины 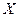в точке 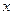называется предел отношения вероятности попадания значений этой величины в интервал 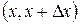к длине 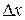отрезка 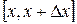, когда последняя стремится к нулю:

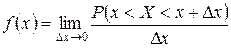. (8.3)

График функции f(х) (плотности распределения) называется кривой распределения.

Интеграл от функции f(х) по промежутку (-∞,х) равен значению функции распределения F(x) для верхнего предела интегрирования, т.е.

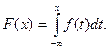(8.4)

Вероятность попадания значений случайной величины Х в интервал 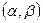равна определенному интегралу от плотности распределения p(x) по отрезку 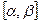, т.е.

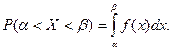(8.5)

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежит всей оси Ох, определяется равенством ,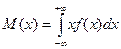

где f(x) – плотность вероятности. Предполагается, что интеграл сходится абсолютно.

Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат Ох, определяется равенством

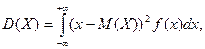
или равносильным равенством

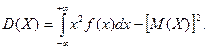
Нормальным распределением, или распределением Гаусса, называется распределение с плотностью вероятностей

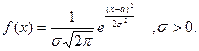(8.6)

Постоянные 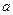и 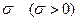называются параметрами нормального распределения.

О случайной величине Х, говорят, что она распределена нормально с

параметрам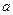и и 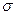, и кратко называют ее нормальной. График функции f(x)

называют нормальной кривой.

Вероятность попадания значений нормальной случайной величины Х в интервал 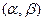определяется формулой

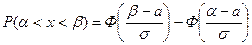(8.7)

где 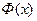- функция Лапласа:

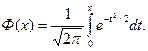(8.8)

Пример 1. В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято 2 детали. Найти функцию распределения дискретной случайной величины, равной числу стандартных деталей в выборке.

Решение. Найдем сначала закон распределения данной случайной величины 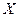. Эта величина может принимать три значения:

, ,

.

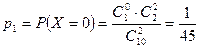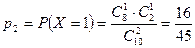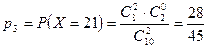Следовательно, закон распределения данной случайной величины можно задать таблицей

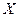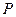i
i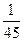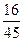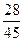

Строим функцию распределения.

1. При .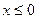

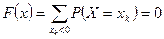2. При .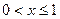

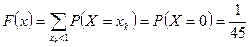3. При .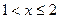

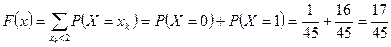4. При .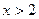

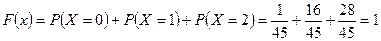Ответ: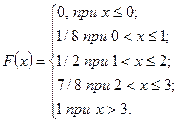

Пример 2. Вес пойманной рыбы подчиняется нормальному закону распределения с параметрами 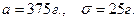Найти вероятность того, что вес одной рыбы будет: а) от 300 до 425 г; б) не более 450 г; в) больше 300 г.

Решение. Пользуемся формулой (8.20), полагая в ней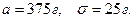

а) 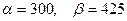, поэтому

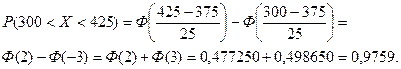
б) Х<450 находим

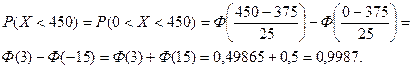
в) Х>300 получаем

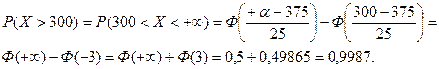
Ответ: а) 0,9759, б) 0,9987, в) 0,9987.