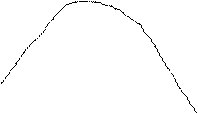
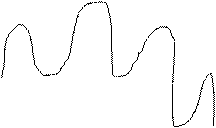
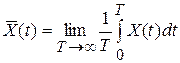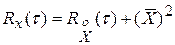Корреляционные функции случайных процессов

Математическое ожидание и дисперсия являются важными характеристиками случайного процесса, но они не дают достаточного представления, какой характер будут иметь отдельные реализации случайного процесса. Рассмотрим рисунок.

X(t) X(t)

m_X(t)+ m_X(t)+3s_X(t)

3s_X(t)

m_X(t)

m_X(t) t

0 a) б)

m_X(t)-3s_X(t) m_X(t)-3s_X(t)

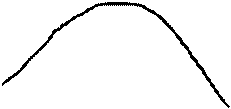
Процесс изображенный на рис. А), от сечения к сечению протекает плавно, а на рис. Б) обладает изменчивостью от сечения к сечению. Поэтому статистическая связь между сечениями в первом случае больше, чем во втором, однако, ни по математическому ожиданию, ни по дисперсии этого установить нельзя.

Для того, чтобы учесть степень изменчивости случайного процесса, необходимо ввести понятие корреляционной (автокорреляционной) функции случайного процесса.

Корреляционной функцией случайного процесса X(t) называют неслучайную функцию двух аргументов R_x(t₁,t₂), которая для каждой пары произвольно выбранных значений аргументов t₁, t₂ равна математическому ожиданию произведения двух случайных величин X(t₁) и X(t₂), соответствующих сечениям случайного процесса:

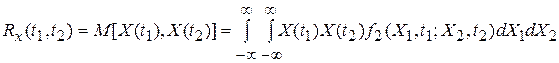
где 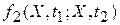- двумерная плотность распределения вероятности.

Корреляционная функция для центрированной случайной составляющей .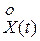

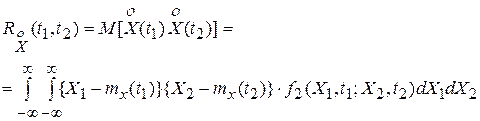
Универсальная характеристика.

Корреляционная функция – универсальная характеристика для случайного процесса. Она определяет зависимость С.В. в последующий момент времени X(t₂) от предшествующего значения X(t₁) в момент времени t₁.

К.Ф. – мера связи между X(t₁) и X(t₂). Случайный процесс в зависимости от того, как изменяется их статистические характеристики с течением времени, делят на стационарный и нестационарный.

Стационарным в узком смысле называют случайный процесс X(t) если его n-мерные функции распределения и плотность вероятности при любом n не зависят от положения начала отсчета времени t, т.е.

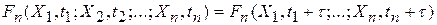
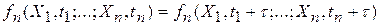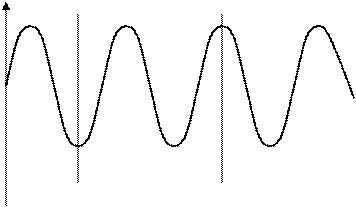
Пример: Установившегося период. колеб.

X(t)

t t+t

Это означает, что два процесса X(t), X(t+t) имеют одинаковые статистические свойства для любого t, т.е. статистические характеристики случайного процесса неизменны во времени (инвариантны относительно временного сдвига t).

Стационарный случайный процесс – это своего рода аналог установившегося процесса в детерминированных системах. Любой переходный процесс – не стационарен (в смысле Хинчина).

Стационарным в широком смысле называют случайный процесс математическое ожидание которого постоянно:

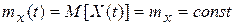
а корреляционная функция зависит только от одной переменной – разности аргументов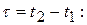

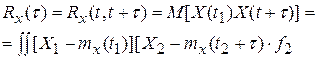
Пример: Сл. пр. U(t) образован реализациями вида

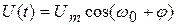
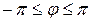
Свойства К.Ф. ст. случ. пр.

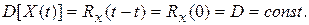
Стационарность в широком смысле вводится тогда, когда в качестве статистических характеристик случайного процесса используется только математическое ожидание и корреляционная функция. Часть теории случайных процессов, которая описывает свойства случайных процессов через его математическое ожидание и корреляционную функцию называют корреляционной теорией случайных процессов.

Для случайных процессов с нормальным законом распределения математическое ожидание и корреляционная функция полностью определяют его n-мерную плотность вероятности f_n(…). Поэтому для нормальных случайных процессов понятие стационарности в широком и узком смысле совпадают.

Пример стационарного случ. процесса

X(t)

t₁ t₂

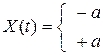“телеграфный сигнал” – одна из реализаций

Из стационарности в узком смысле следует стационарность в широком смысле.

В теории случайных процессов пользуются двумя понятиями средних значений.

– это среднее по множеству (или математическое ожидание) - 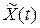, которое определяется на основе наблюдений над множеством реализаций случайного процесса 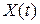в один и то же момент времени. Обозначают:

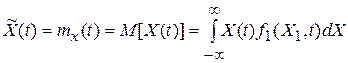В общем случае среднее значение по множеству является функцией времени t.

2.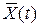- это среднее значение по времени, которое определяется на основе наблюдения за отдельной реализацией случайного процессаX(t) на протяжении достаточно длительного времени Т. Обозначают:

<X(t)>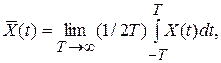

если предел существует.

Среднее значение по времени в общем случае различно для отдельных реализаций X_i(t) множества X(t), определяющих случайный процесс.

Вообще для одного и того же случайного процесса X(t) среднее по множеству 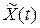и среднее по времени 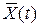различны, однако есть сл. стац. проц. (эргодические стационарные процессы), для которых среднее по множеству совпадает со средним по времени: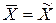

Такие стационарные случайные процессы называются эргодическими.

Ст. сл. пр. обладают замечат. св-м Ñ эргод. гипотезой. Т.к. вероятн. хар. Стационарного процесса со временем не изм., то длит набл. X_i(t) на 1 объекте даст в среднем такую же картину, как и большое число наблюдений, сделанные на n объектах.

Не всякий стационарный процесс является эргодическим.

Под эргодическим случайным процессом будем понимать процесс, когда все его статистические свойства можно определить по одной единственной, достаточно продолжительной реализации процесса X_i(t).

Равенство 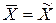вытекает из эргодической теоремы, которая доказана для некоторых стационарных случайных процессов. Физический смысл эргодической теоремы глубок и имеет практическое значение для вычисления статистических характеристик. Для определения статистических характеристик эргодических стационарных случайных процессов можно наблюдать одну систему в печени длительного времени. Этим пользуются при определении корреляционной функции стационарного случайного процесса по одной реализации.

Эргодическая гипотеза позволяет упростить все расчеты и эксперименты, позволяет для определения М.О., D, s испытывать вместо параллельных исп. n систем, пользуются испыт. X(t) одной реализации в течении длит t.

Из определения видно, что корреляционная функция представляет собой среднее значение по множеству. В соответствии с эргодической теоремой для стационарного случайного процесса корреляционную функцию можно определить как среднее по времени от произведения X(t) и X(t=t),т.е.

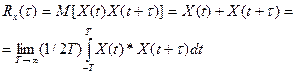(1)

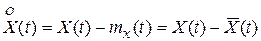
Центрированная корреляционная функция эргодического стационарного случайного процесса

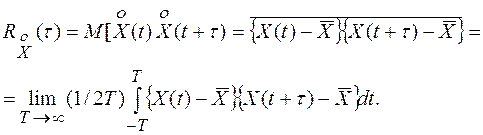(2)

Между R_x(t) и 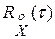существует связь

(3)

Основываясь на свойстве эргодичности, можно дисперсию D_X определить как среднее по времени от квадрата центрированного случайного процесса.

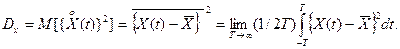(4)

Из (2) и (4) следует, что дисперсия случайного процесса равна начальному значению центрированной корреляционной функции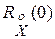

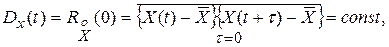(5)

т.к. рассм. конкр. мом.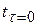

Учитывая (3), можно установить связь между дисперсией и корреляционной функцией R_x(t), т.е.

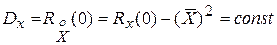(6)

Из (5) и (6) имеем

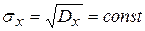(7)

Аналогично К.Ф. вводится понятие В.К.Ф. 2-х с.п. X(t) и Y(t)

Взаимная корреляционная функция – характеризует статистические свойства двух случайных процессов X(t) и Y(t) и определяется

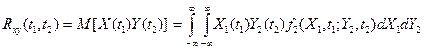(8)

Если 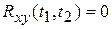, то X(t) и Y(t) не коррелированны, если 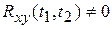, то X(t) и Y(t) коррелированные С.Ф.

Согласно эргодической теоремы вместо (8) можно записать для С.С.П.

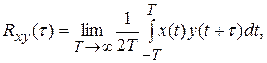(9)

где x(t), y(t) – любые реализации стационарного случайного процесса X(t) и Y(t) соответственно.

Если t=0, то имеем R_xy(0), которая характеризует связь случайных процессов в один и тот же момент времени.

Если X(t) и Y(t) статистически не связаны 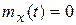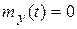и имеют равное нулю среднее значение – то 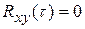. Обратный вывод не вегда справедлив. Для процессов с нормальным распределением обратный закон справедлив.