2015-03-07
2428
Известны следующие параметры механизма (рис. 2.7):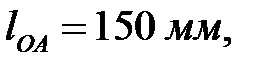 
, 
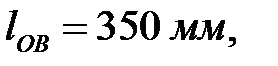
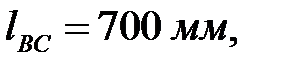
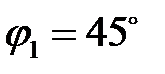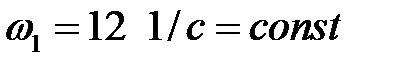, направление вращения кривошипа – против часовой стрелки.
Требуется определить линейные скорости и ускорения точек механизма, а также угловые скорости и ускорения звеньев.
2.3.1 Построение плана положений механизма
Выражаем все длины звеньев в метрах:
.
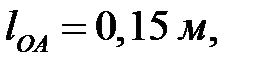
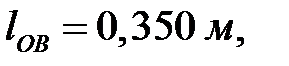
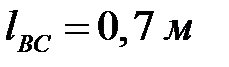Определяем масштабный коэффициент длин, представляющий собой отношение действительной длины в метрах к длине отрезка на чертеже в миллиметрах. Изображаем длину кривошипа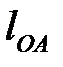 
на чертеже отрезком 
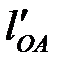, равным, например, 30 мм. Тогда масштабный коэффициент будет иметь величину
.
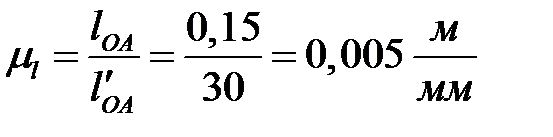Остальные длины звеньев, изображенные на чертеже, будут иметь следующие значения
, 
.
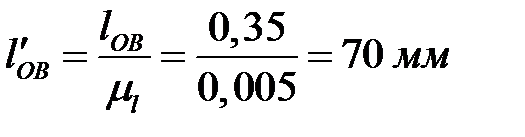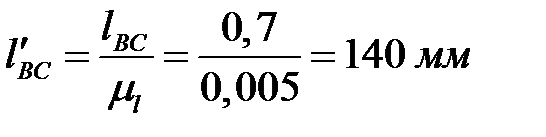Из произвольной точки О под углом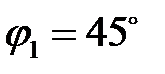 
откладываем отрезок 
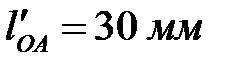, получая точку А, которую соединяем с точкой В, отстоящую от точки О на расстоянии 70 мм. Точку С получаем, откладывая расстояние 
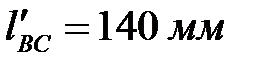. Прямоугольником изображаем камень.
Аналогичным образом можно построить и другие положения механизма, которые отличаются величинами угла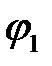 
.
2.3.2 Построение плана скоростей
Определяем скорость точки А, принадлежащей кривошипу 1 и камню 2
.
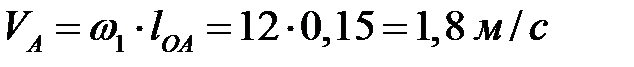Находим масштабный коэффициент скоростей, для чего полученную величину делим на длину вектора этой скорости, выбранную равной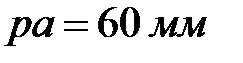 
.
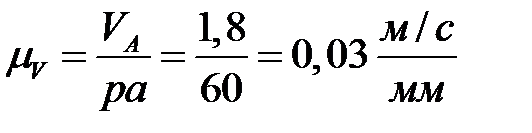Из произвольной точки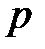 
(рис. 2.8) – полюса скоростей, проводим вектор 
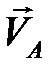, который перпендикулярен кривошипу и направлен в сторону его вращения. Длина этого вектора равна 60 мм. Скорость точки 
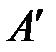, принадлежащей кулисе 3, находим графически, используя векторные уравнения
, 
.
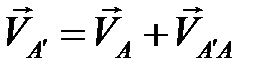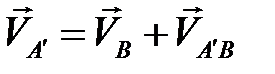Так как скорости точек 
и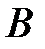 
равны нулю, то точки 
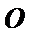и 
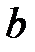помещаем в полюсе. Система уравнений решается графически следующим образом. Из точки 
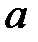проводим линию, параллельную кулисе ВС, а из полюса 
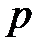– прямую, перпендикулярную кулисе. На пересечении получаем точку 
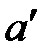. Ставим две стрелки, получая скорост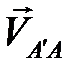и 
и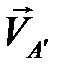 
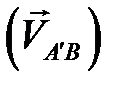. Для нахождения точки 
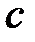на плане скоростей воспользуемся выражением
.
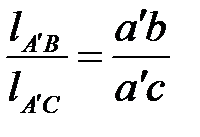Замеряем на рисунке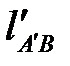 
, 
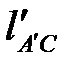и 
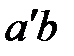, находим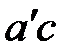 
.
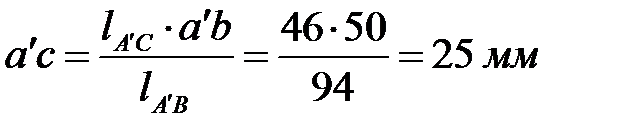Точку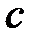 
соединяем с полюсом, получая скорость 
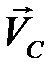. Численные значения полученных скоростей находим через коэффициент 
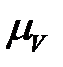, замеряя длины векторов
, 
,
.
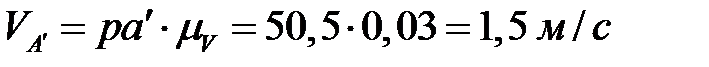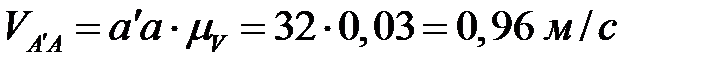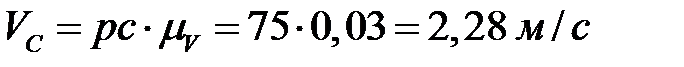Вычисляем угловую скорость кулисы и камня
.
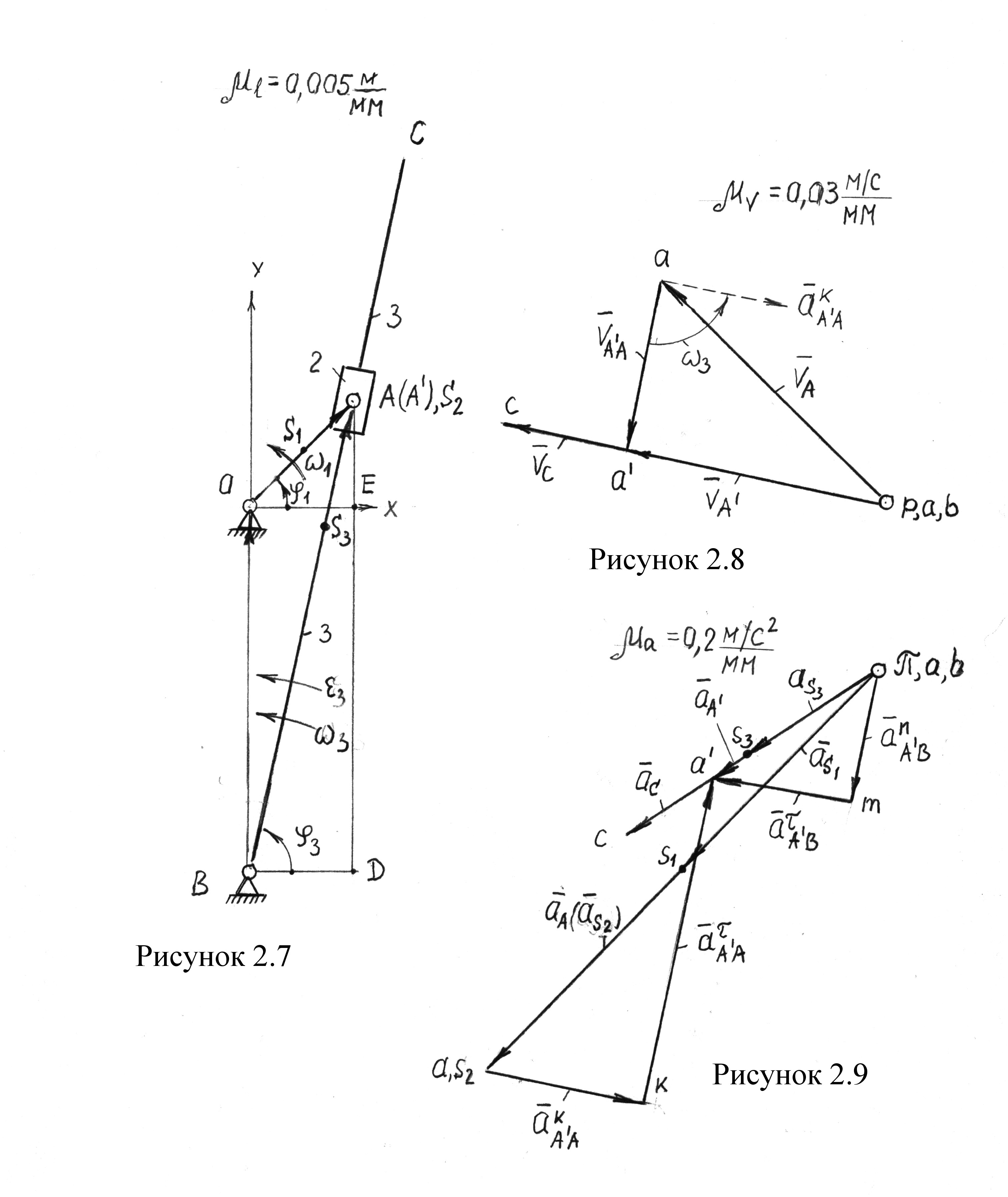
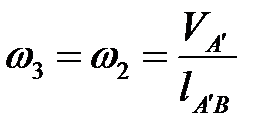Здесь величина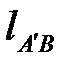 
определяется умножением замеренной величины 
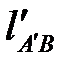на масштабный коэффициент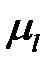 
.
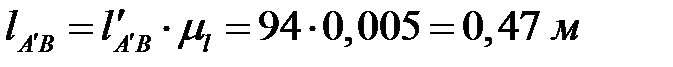Следовательно,
.
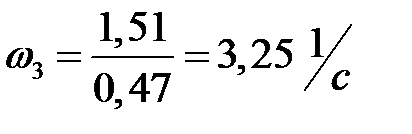2.3.3 Построение плана ускорений
Определяем ускорение точки А.
.
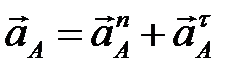Так как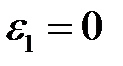 
, то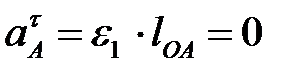 
.
Тогда
.
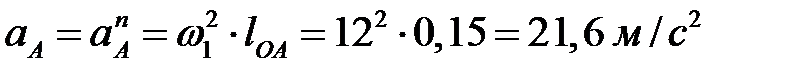Масштабный коэффициент ускорений можно найти путем деления ускорения точки А на длину вектора на чертеже, выбранную нами равной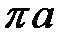 
=108 мм.
.
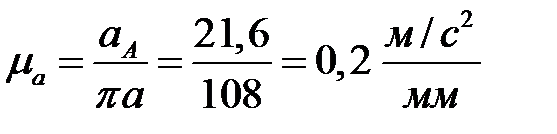Ускорение точки А направлено от точки А к центру О параллельно кривошипу.
Из произвольной точки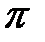 
– полюса ускорений (рис. 2.9) проводим вектор 
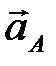длиной 108 мм. Ускорение точки 
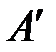кулисы находим графо-аналитически, решая систему векторных уравнений
, 
.
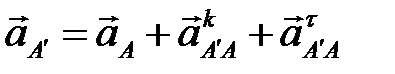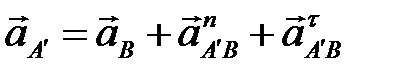Ускорения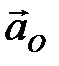 
=0 и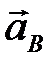 
=0, точки 
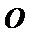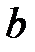и помещаем в полюсе. Определяем по модулю ускорения 
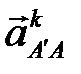и 
,
.
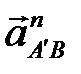
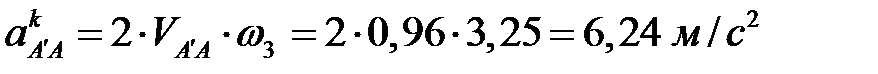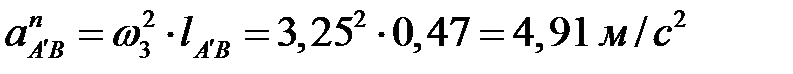Находим длины векторов этих ускорений
, 
.
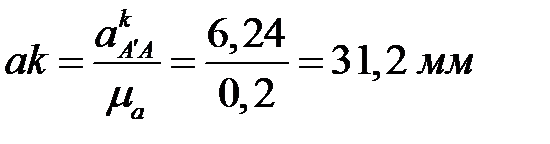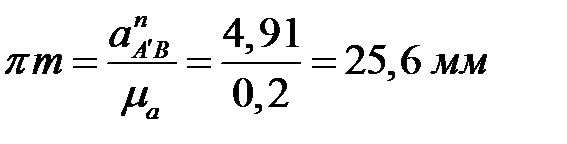Для определения направления ускорения Кориолиса нужно вектор 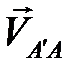(рис. 2.8) повернуть по направлению 
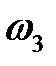, т.е. против часовой стрелки, на 
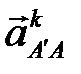. Следовательно, будет направлен вправо перпендикулярно кулисе. Из точки 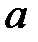проводим ускорение 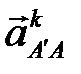, а из полюса – ускорение 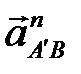, которое идет параллельно кулисе ВС от точки 
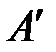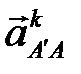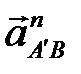к точке В. Перпендикулярно к и проводим прямые, которые пересекаются в точке 
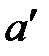. Эту точку соединяем с полюсом, получая векторы 
, 
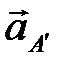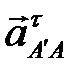и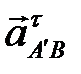 
.
Точку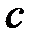 
на плане ускорений определяем, решая равенство
, 
.
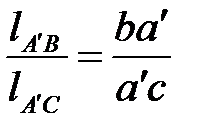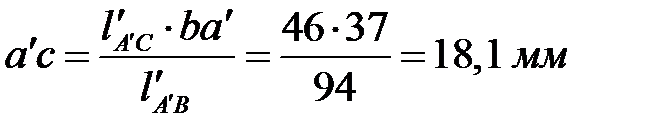Обозначаем вектор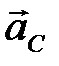 
стрелкой.
Следует отметить, что если длина какого-то вектора оказывается меньшей 3 мм, то этот вектор на плане ускорений отмечается точкой, около которой ставится обозначение этого ускорения.
Точк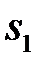и 
и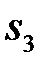 
находятся в серединах отрезков 
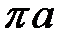и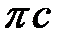 
, а точка 
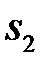совпадает с точкой 
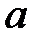. Соединяя точк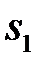и и 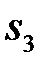с полюсом, получаем векторы 
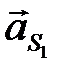и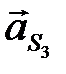 
. Замеряем длины всех неизвестных векторов ускорений и через масштабный коэффициент определяем их модули
,
,
,
,
,
,
.
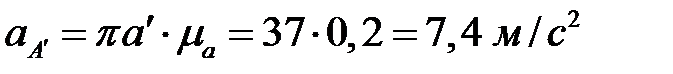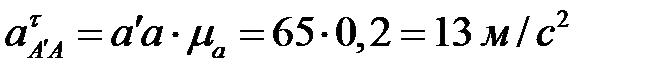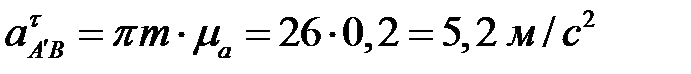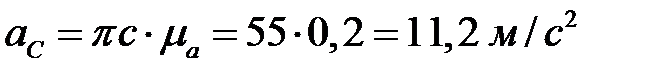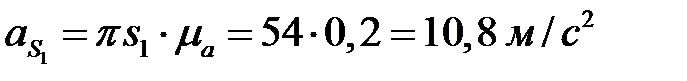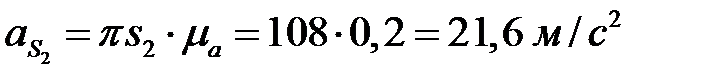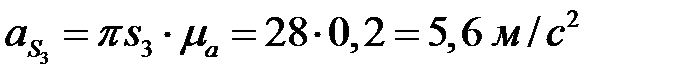Вычисляем угловое ускорение кулисы, которое равно угловому ускорению камня
.
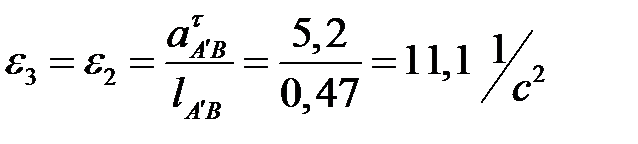Перенося вектор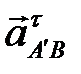 
в точку 
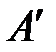механизма, находим, что угловое ускорение направлено против часовой стрелки. Отмечем его дуговой стрелкой.
