2015-03-07
1306
Известны следующие параметры механизма (рис 3.7):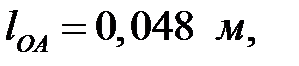 
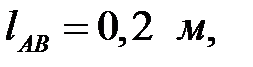
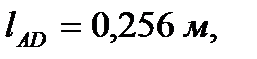
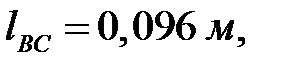
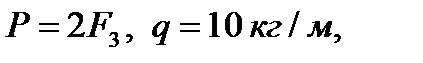
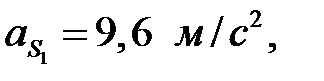
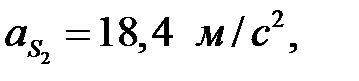
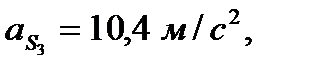
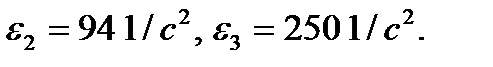(Все ускорения берутся из первого листа курсовой работы).
Требуется определить реакции в кинематических парах и уравновешивающую силу.
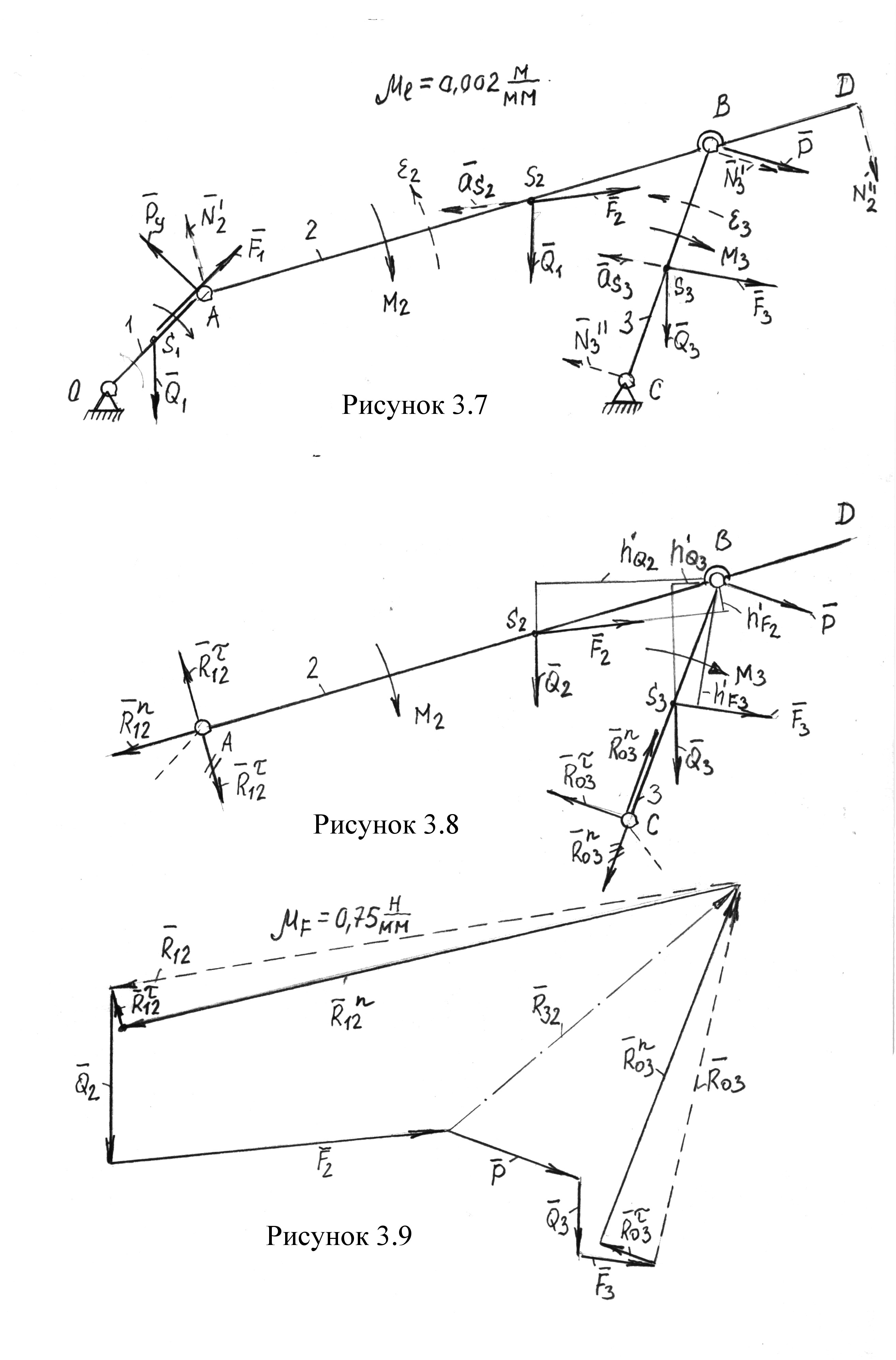
Изображаем механизм в заданном положении с обозначением масштабного коэффициента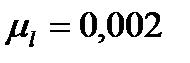 
м/мм, который в данном случае обозначает, что механизм уменьшен в два раза. На механизм действуют следующие силы.
1.Сила полезного сопротивления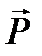 
, указываемая в задании. Она приложена в точке В коромысла 3 и направлена ему перпендикулярно.
2.Силы тяжести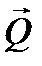 
, определяемые через массы звеньев, которые можно условно найти по формуле 
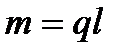, где q –масса единицы длины звена, l –длина звена
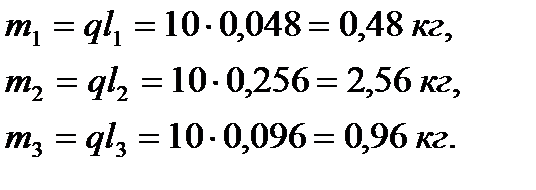
Следовательно,
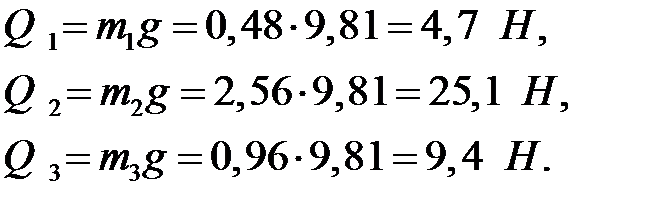
Силы тяжести прикладываются в центрах масс S1, S2, S3 и направлены вертикально вниз.
3.Силы инерции звеньев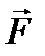 
, определяемые по формуле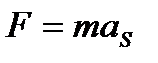 
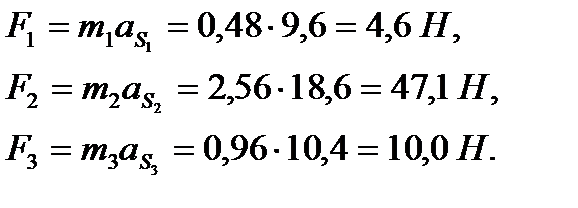
Эти силы прикладываются в центрах масс и направлены в стороны, обратные ускорениям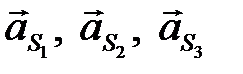 
. (Желательно план ускорений с первого листа перенести на второй лист).
4.Момнеты сил инерции М, которые можно найти по формуле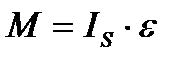 
, где IS –моменты инерции звеньев относительно центральных осей
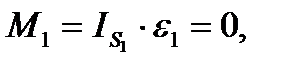т.к.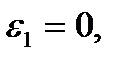 
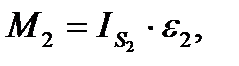
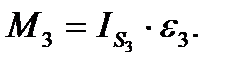
Моменты инерции звеньев определяем по формуле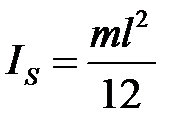 
,
.
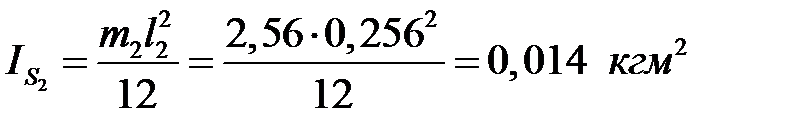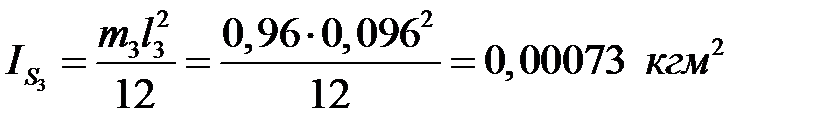Следовательно,
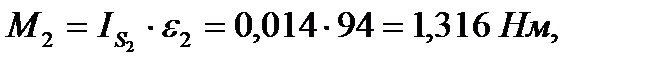
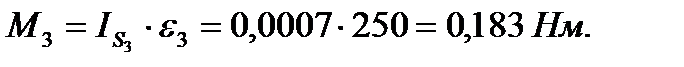
Моменты сил инерции направлены в стороны, обратные угловым ускорениям.
5. Уравновешивающая сила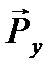 
, прикладываемая в точке А кривошипа 1 и направленная перпендикулярно ему. Пусть в нашем примере она направлена влево.
Все силы и моменты указываем на механизме, причем длины векторов берем произвольно.
Изображаем отдельно структурную группу, состоящую из шатуна 2 и коромысла 3 (рис. 3.8). Реакции в точках А и С раскладываем на две составляющие, одну из которых направляем по звену (в ту или иную сторону), а вторую – перпендикулярно звену (также в ту или иную сторону). Из точки В на все силы проводим перпендикуляры, которые являются плечами этих сил. Замеряем каждое плечо в миллиметрах и умножаем на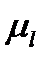 
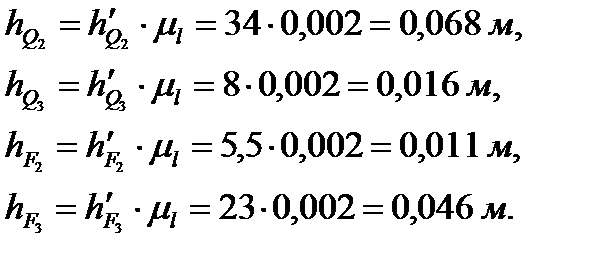
Рассматриваем равновесие звена 2, отбрасывая мысленно звено 3, и записываем уравнение моментов относительно точки В
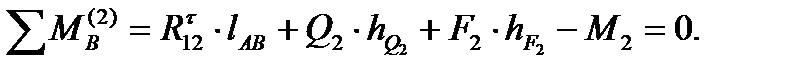
Откуда
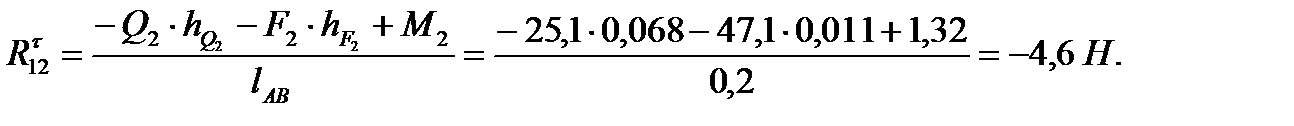
Так как эта сила оказалась отрицательной, то на чертеже группы нужно вектор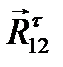 
перечеркнуть (стирать нельзя!) и направить в другую сторону.
Отбрасываем мысленно звено 2 и записываем уравнение равновесия звена 3 относительно той же точки В
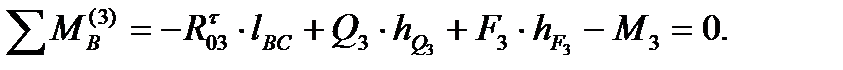
Откуда
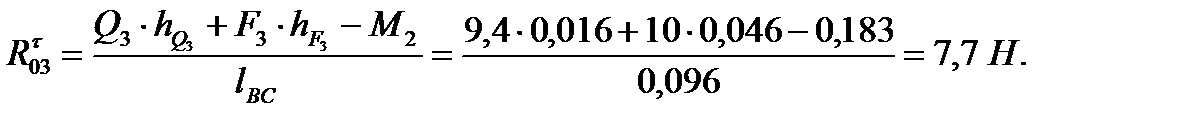
Используем графическое условие равновесия двух звеньев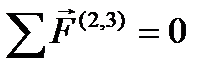 
и строим силовой многоугольник в масштабе 
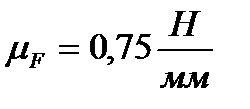. Вычисляем длины векторов сил
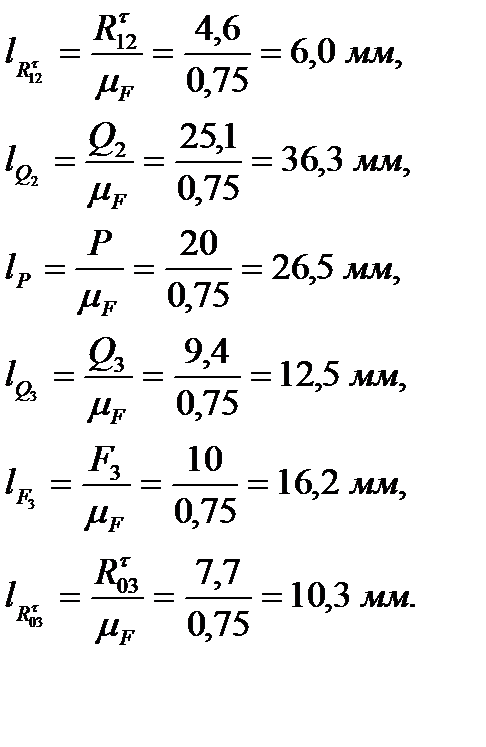
Начинаем построение с силы 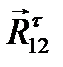(рис. 3.9), отмечая начало ее точкой. Далее силы идут в любом порядке, но желательно, чтобы сначала шли все силы одного звена, а затем силы, действующие на другое звено. Последняя сила – это 
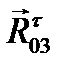. Если длина вектора одной из сил оказалась менее 3 мм, то вместо нее ставим точку с обозначением этой силы. В начале построения к силе 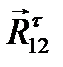проводим перпендикуляр и в конце силы 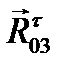также к ней проводим перпендикуляр. Пересечение перпендикуляров дает силы 
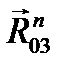и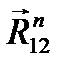 
, причем сила 
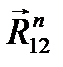идет в начало силы 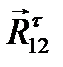, а вектор 
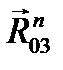идет из конца силы 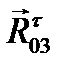. Таким образом, стрелки в многоугольнике идут одна за другой. Сравниваем направления векторов на чертеже (рис. 3.8) и в силовом многоугольнике (рис. 3.9). Замечаем, что сила 
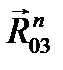на рис. 3.8 направлена в другую сторону. Поэтому мы её перечеркиваем и поворачиваем на 180˚. Силы в шарнирах А и С попарно складываем: 
, 
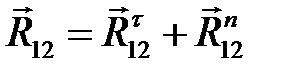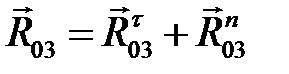. (На рис. 3.8 силы складывать нельзя!) Сила 
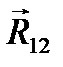должна идти навстречу силе 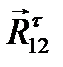, а сила 
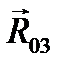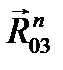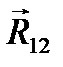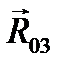--навстречу . Замеряем длины векторов и , умножаем результаты на 
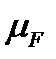, получаем модули этих сил
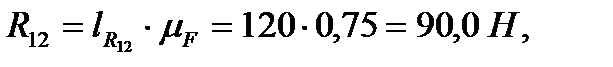
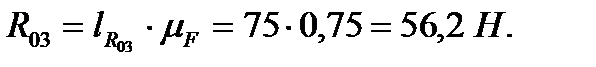
Чтобы получить реакцию в шарнире В, нужно рассмотреть равновесие одного звена, например - второго. Для этого начало силы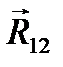 
(рис. 3.9) нужно соединить с концом силы 
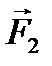. Получаем вектор 
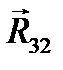, который идет в начало силы 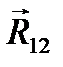. Замеряем длину этого вектора и умножаем на 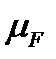. Получаем модуль этой силы
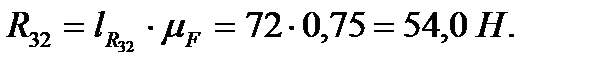
Изображаем отдельно кривошип 1 со всеми силами (рис. 3.10), причем реакцию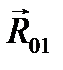 
направляем пока произвольно, а сила 
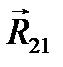направлена в сторону, обратную силе 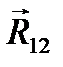, т.е. 
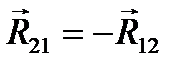.Из точки О проводим перпендикуляры ко всем силам, замеряем их и умножаем на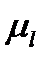
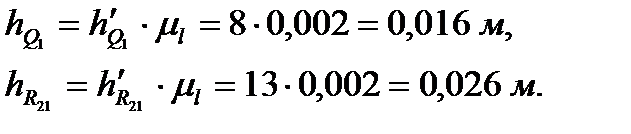
Рассматривая равновесие кривошипа, записываем уравнение моментов относительно точки О
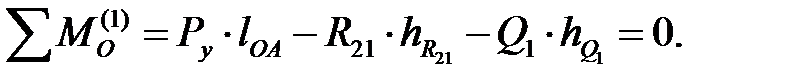
Откуда
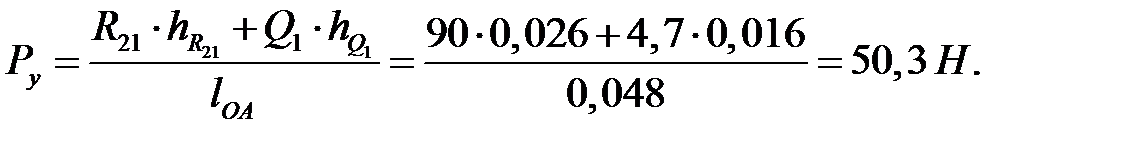
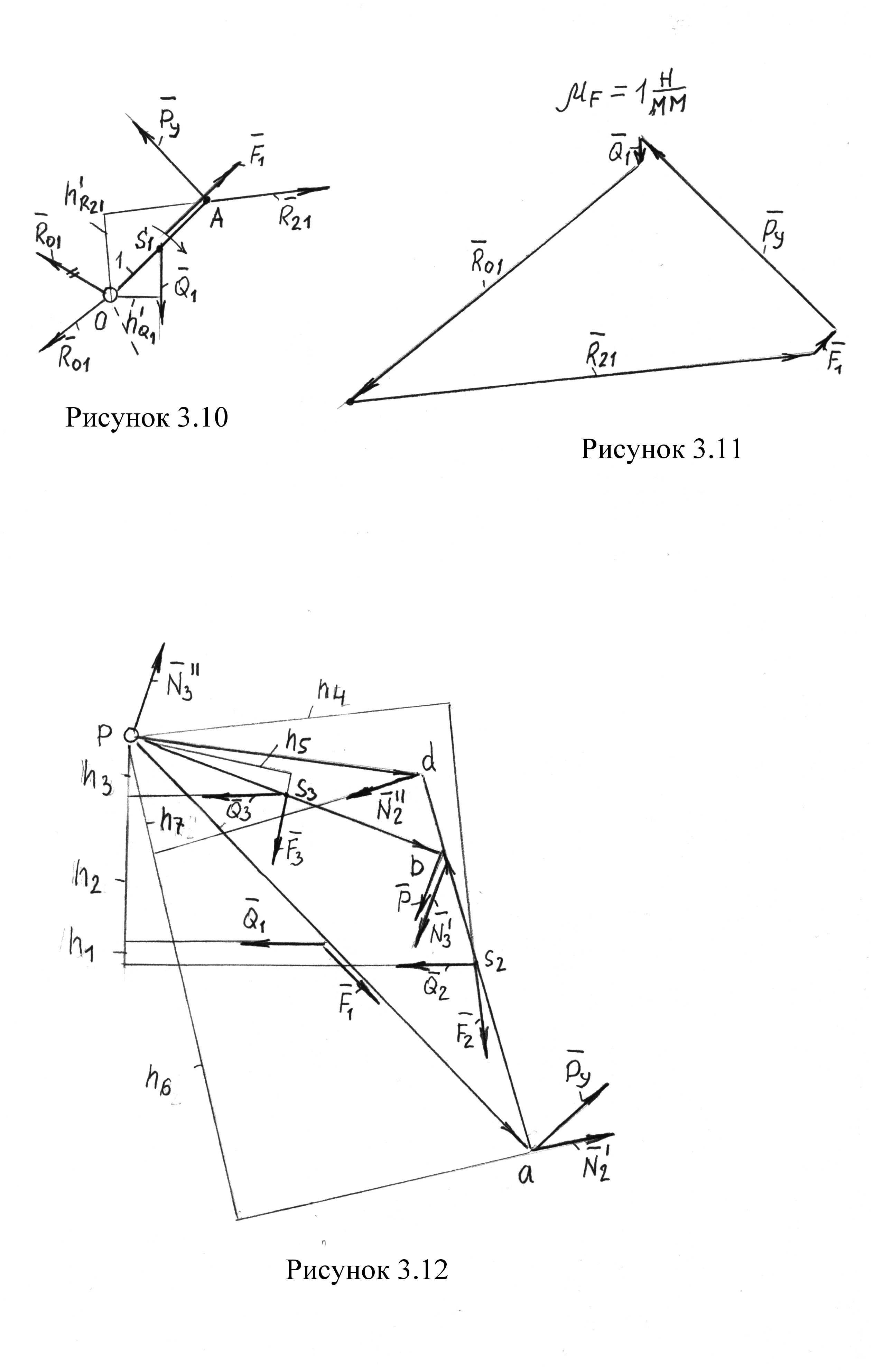
Строим силовой многоугольник для кривошипа в масштабе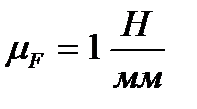 
(рис. 3.11). Находим длины векторов
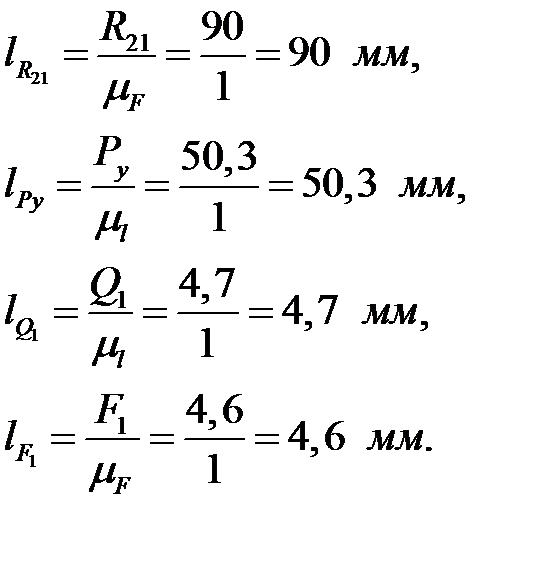
Замыкающий вектор многоугольника представляет собой реакцию 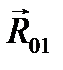, которая направлена в начало первой силы. Измеряем длину этого вектора и умножаем на масштаб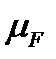
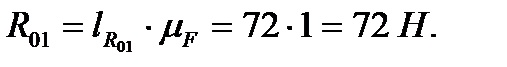
Вектор 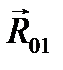на рис. 3.10 перечеркиваем и направляем так, как он идет в многоугольнике.
Для поверки точности расчетов и построений найдем уравновешивающую силу по методу Жуковского. Моменты сил инерци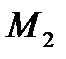и 
и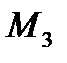 
заменяем парами сил 
, 
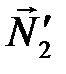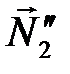и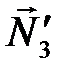 
, 
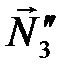(рис 3.7), действующих, например, в точках А, В, С и D. При этом направление пар сил должны совпадать с направлением моментов. Найдем величины этих сил
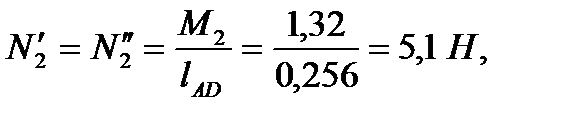
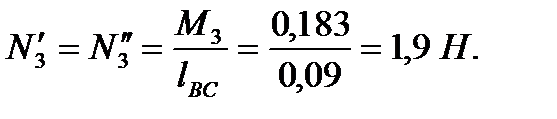
Переносим с первого листа курсовой работы план скоростей, на который помещаем все внешние силы (рис. 3.12), приложив их в соответствующие точки и повернув на 90˚ в ту или иную сторону. В нашем случае все силы повернуты по часовой стрелке. Из полюса р проводим к силам перпендикуляры, которые являются плечами сил. Замеряем длины перпендикуляров и записываем уравнение моментов относительно полюса
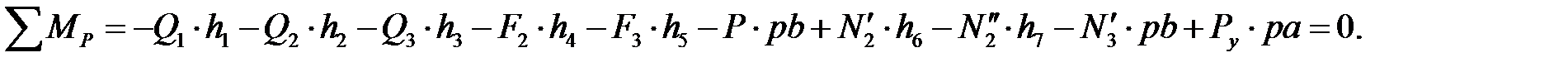Откуда
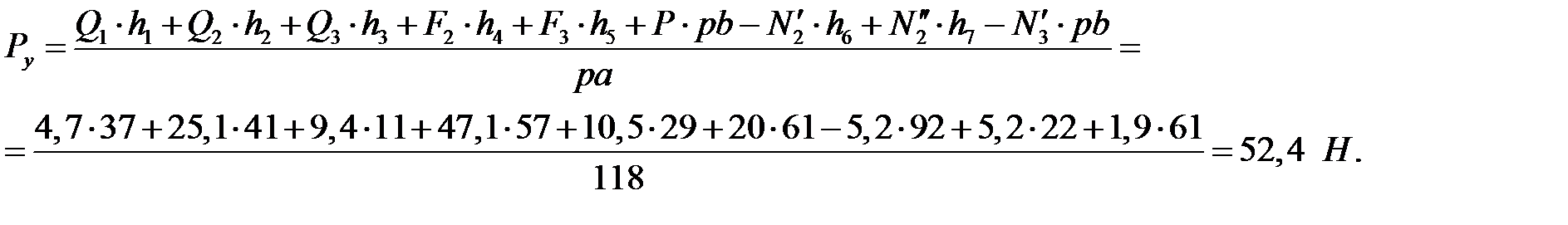
Сравнение результатов, полученных двумя способами, говорит о том, что погрешность вычислений и построений незначительна.
