Теорема об изменении количества движения материальной точки или МС

1. Для материальной точки:

при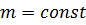

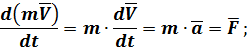
после разделения переменных

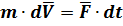
и интегрирования получаем:

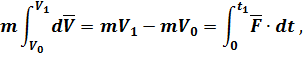
где 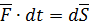– элементарный импульс силы.

После интегрирования от 0 до 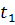получается импульс силы :

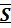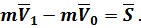
2. Для МС из 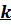точек:

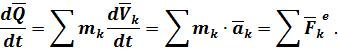
После интегрирования от 0 до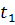

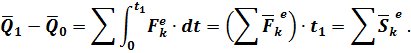
ПОНЯТИЕ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ

Относительно центра (рис. 67).

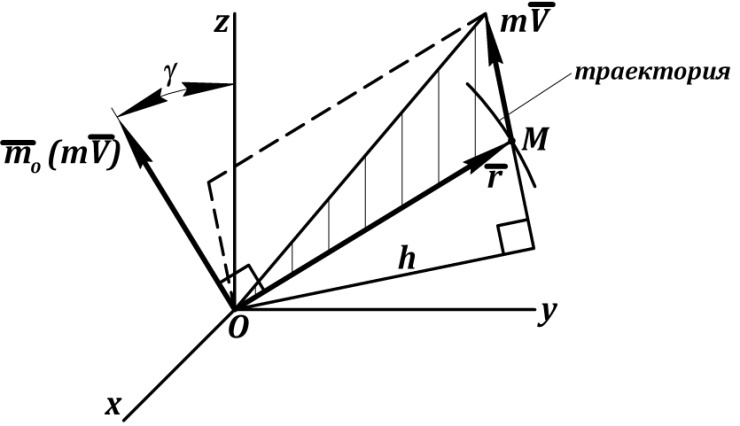
Рис. 67. Момент количества движения точки относительно центра

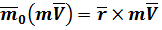
– векторное произведение, где:

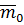– функция момента;

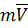– аргумент функции;

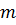– масса точки.

Абсолютная величина

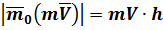
– площадь прямоугольника со сторонам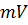и и .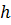

Относительно оси (рис. 67).

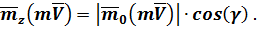
8. ПОНЯТИЕ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ (КИНЕТИЧЕСКОГО МОМЕНТА)