2015-03-08
258
Ранее было получено выражение для кинетического момента
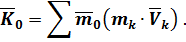
Тогда изменение этой величины будет
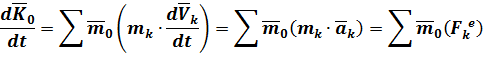
– сумма моментов внешних сил относительно центра 
.
Относительно оси.
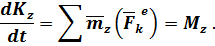
Тогда
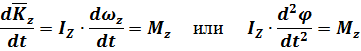
– это дифференциальное уравнение вращательного движения твёрдого тела вокруг оси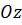 
.
Так как
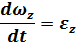
– угловое ускорение, то
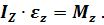
Последнее равенство показывает, что при данном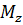 
чем больше момент инерции тела 
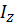, тем меньше угловое ускорение 
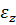, и наоборот.
Следовательно, момент инерции тела действительно играет при вращении ту же роль, что и масса при поступательном движении, т.е. является мерой инертности тела при вращении.
При этом:
¾ если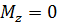 
, то 
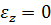и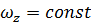 
, тело вращается равномерно;
¾ если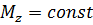 
, то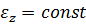 
, 
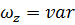, тело вращается равнопеременно.
