Определим разность напоров, необходимую для движения неньютоновской (бинганомовской) жидкости, заполняющей горизонтальный трубопровод длиной L и диаметром d. Давление в начале и конце трубопровода обозначим р1 и р2, плотность жидкости ρ, ее начальное напряжение сдвига τ0. Уравнение равновесия, составленное для системы сил, действующих на заданный объем жидкости будет иметь вид:
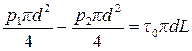 , (4.1)
, (4.1)
Разность давлений на концах трубопровода будет равна:
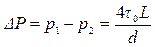 , (4.2)
, (4.2)
Разность напоров в тех же сечениях:
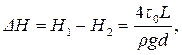 (4.3)
(4.3)
Таким образом, если выполняется условие:
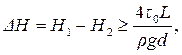 (4.4)
(4.4)
то жидкость в трубопроводе будет двигаться, причем в зависимости от разности напора возможны три режима ее движения: структурный, ламинарный и турбулентный. При структурном режиме весь поток жидкости движется с одинаковой скоростью по всему поперечному сечению. Увеличение разности напора ΔН приводит к увеличению скорости движения жидкости. В пристенной части трубопровода развивается ламинарный режим, а в центральном ядре жидкость движется как твердое тело. Такой режим движения, характеризующийся наличием центрального ядра, называется структурным.
Радиус центрального ядра рассчитывается по формуле:
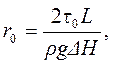 (4.5)
(4.5)
При дальнейшем возрастании ΔН область ламинарного режима будет расширяться, а размеры центрального ядра уменьшаться. Наступит момент, когда структурный режим перейдет в ламинарный (r0 = 0). Однако в практике наиболее часто встречающийся режим движения жидкости – турбулентный. В действительности турбулентность начинает зарождаться в потоке еще при наличии центрального ядра, поэтому полностью ламинарного режима обычно не существует и структурный режим переходит непосредственно в турбулентный.
Формула для расчета распределения скоростей при структурном режиме имеет вид:
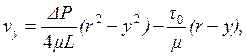 (4.6)
(4.6)
где μ - пластическая вязкость жидкости, Па·с.
Кривая скоростей, соответствующая формуле 4.6, представлена на рис. 4.1. Она состоит из двух частей: двух параболических ветвей у стенок в зоне ламинарного режима и прямолинейного участка в центральном ядре.
Для определения скорости движения центрального ядра в формуле 4.6 необходимо принять у = r0, при этом получим следующую формулу:
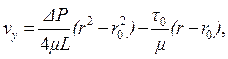 (4.7)
(4.7)
В частном случае, когда τ0 = 0, выражение 4.7 превращается в известную в гидравлике формулу Стокса для ламинарного режима (на рис. 4.1 ей соответствует пунктирная линия).
Зона ламинарного режима
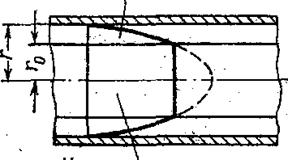
Центральное ядро
Рис. 4.1 Распределение скоростей при структурном режиме потока
Расход жидкости при структурном режиме рассчитывается по формуле Букингема:
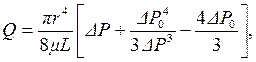 (4.8)
(4.8)
где: ΔР - приложенная разность давлений; ΔР0 - разность давлений, соответствующая началу движения жидкости, вычисляемая по формуле 4.2.
Так как выражение 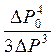 представляет малую величину при значительном перепаде давлений, то им пренебрегают, и формула Букингема принимает более простой вид:
представляет малую величину при значительном перепаде давлений, то им пренебрегают, и формула Букингема принимает более простой вид:
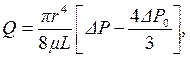 (4.9)
(4.9)
Из полученной формулы 4.9 путем математических преобразований получим зависимость для расчета ΔР:
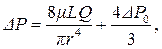 (4.10)
(4.10)
Если в выражение 4.10 вместо ΔР0 подставить формулу 4.2, то после ряда подстановок и преобразований получим формулу для определения потери напора:
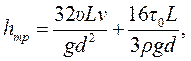 (4.11)
(4.11)
где υ - кинематическая вязкость жидкости, м2/с; v - средняя скорость движения жидкости, м/с; d - диаметр трубопровода, м.
Коэффициент гидравлического сопротивления определяется по формуле:
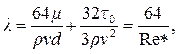 (4.12)
(4.12)
где Re* - обобщенный критерий Рейнольдса.
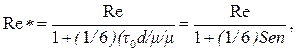 (4.13)
(4.13)
где Sen = (τ0 ·d) / (μ· υ) критерий Сен-Венана - характеризует пластические свойства жидкости.
Расчет потери напора на трение при движение ньютоновских жидкостей определяется по формуле Дарси – Вейсбаха:
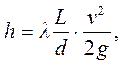 (4.14)
(4.14)
Таким образом, при течении по трубам вязко-пластичных жидкостей, при ламинарном и структурном режимах, потери напора на трение по длине потока можно определять по формуле Дарси- Вейсбаха. При этом коэффициент гидравлического сопротивления λ следует рассчитывать по формуле 4.12.
При турбулентном режиме для определения коэффициента λ применяют формулу типа:
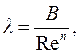 (4.15)
(4.15)
где коэффициент В и показатель степени n устанавливаются экспериментальным путем.
Режим течения неньютоновских жидкостей устанавливается по критическому значению обобщенного числа Рейнольдса. При практических расчетах определяют критическую скорость потока по формуле:
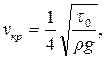 (4.16)
(4.16)
Сравнивая критическую скорость υкр со средней скоростью υ потока, устанавливают характер режима: при υ< υкр – режим структурный, при υ> υкр – турбулентный.
Течение по трубам реологически сложных дисперсионных систем, к которым относятся мясопродукты, происходит при условии создания в продукте давлений, достаточных для преодоления внутренних и внешних сопротивлений.
Поэтому в основе реодинамических (гидравлических) расчетов трубопроводов лежит определение напряжений, оказывающих противодействие при движении продукта (потери давления) по прямым участкам труб и в местных сопротивлениях. В некоторых случаях расчет сводится к определению диаметра трубопровода или расхода.
Общее давление вытеснения 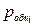 , Па, необходимое для перемещения транспортируемой продукции (массы) определяют по формуле:
, Па, необходимое для перемещения транспортируемой продукции (массы) определяют по формуле:
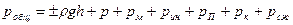 , (4.17)
, (4.17)
где 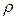 - плотность перекачиваемой массы, кг/м3; h - высота нагнетания продукта, м;
- плотность перекачиваемой массы, кг/м3; h - высота нагнетания продукта, м; 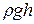 - потери давления, при подъеме массы на заданную высоту, Па;
- потери давления, при подъеме массы на заданную высоту, Па;
р - потери давления по длине трубопровода, Па; 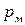 - потери давления в местных сопротивлениях, Па;
- потери давления в местных сопротивлениях, Па; 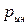 - инерционные потери давления, обусловлены неравномерностью движения, Па;
- инерционные потери давления, обусловлены неравномерностью движения, Па; 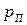 - потери давления на преодоление противодавления, Па;
- потери давления на преодоление противодавления, Па; 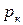 - потери давления на создание кинетической энергии потока, Па;
- потери давления на создание кинетической энергии потока, Па; 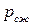 - потери давления на сжатие продукта, Па.
- потери давления на сжатие продукта, Па.
В отдельных случаях количество членов в уравнениях может быть разное, в частности, при отсутствии сопротивления перемещаемой массы, на выходе из трубопроводной системы, значение 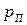 = 0, при отсутствии подъема массы на некоторую высоту
= 0, при отсутствии подъема массы на некоторую высоту 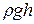 = 0 и при свободном течении массы по трубе
= 0 и при свободном течении массы по трубе 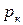 = 0.
= 0.
При проведении расчета трубопроводов общими являются уравнения опредления расхода (подачи), которые определяются из условий непрерывности:
- объемный расход: 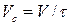 , м
, м 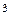 /с;
/с;
- массовый расход: 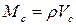 , кг/с; (4.18)
, кг/с; (4.18)
- весовой расход: 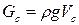 Н/с.
Н/с.
где 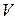 - объем продукта, проходящего через трубопровод, м
- объем продукта, проходящего через трубопровод, м 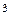 ;
; 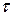 - время, с;
- время, с;
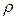 - плотность продукта, кг/м
- плотность продукта, кг/м 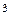 ;
; 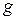 - ускорение свободного падения, м/с
- ускорение свободного падения, м/с 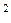 .
.
Объемный расход связан с геометрическими размерами трубопровода и кинематикой течения продукта в нем, и рассчитывается по формуле:
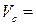 wF=w
wF=w 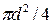 =w
=w 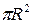 , (4.19)
, (4.19)
где w - средняя скорость движения продукта, м/с; F - площадь живого сечения трубопровода, м 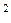 (F равна площади сечения продукта, которая нормальна вектору средней скорости); d -внутренний диаметр трубопровода, м; R - внутренний радиус трубопровода, м.
(F равна площади сечения продукта, которая нормальна вектору средней скорости); d -внутренний диаметр трубопровода, м; R - внутренний радиус трубопровода, м.
Продукт считают сплошной, неразрывной средой с непрерывным распределением физических свойств, деформаций и скоростей деформаций, что позволяет использовать аппарат математического анализа, приложенного к непрерывным функциям. При расчете трубопроводного транспорта определяющую роль играют три группы факторов: геометрические - площадь живого сечения (диаметр); кинематические - средняя скорость потока или объемный расход; динамические - давление в начале трубы или потери давления вдоль трубы. К динамическим факторам относятся также реологические характеристики и плотность, которые должны быть известны для каждого продукта.
В соответствии с этим на практике имеют место три случая расчета трубопроводов, когда определяют одну неизвестную величину, если две остальные известны: первый случай - давление в начале трубы (потери давления или напора вдоль трубы); второй - расход жидкости (подача) или средняя скорость продукта; третий - диаметр трубы (площадь живого сечения). В первом и во втором случаях диаметр можно определить из условий оптимальности по стоимостным показателям. Условно можно выделить четвертый случай, когда при известных трех факторах определяют реологические характеристики.
В выборе метода расчета существенное значение имеет режим движения продукта по трубе, оцениваемый критерием Рейнольдса (Re). Он представляет собой безразмерное числовое значение, пропорциональное отношению кинетической энергии потока mw 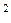 / 2 к работе сил вязкого сопротивления Рl (где m -масса, w - среднеобъемная скорость, Р - сила сопротивления):
/ 2 к работе сил вязкого сопротивления Рl (где m -масса, w - среднеобъемная скорость, Р - сила сопротивления):
Re = 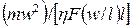 =
= 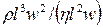 =
= 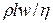 =
= 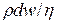 =
= 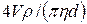 , (4.20)
, (4.20)
где l - характерный линейный размер (для круглой трубы - диаметр d), м;
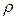 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3; 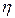 - динамический коэффициент вязкости, Па·с.
- динамический коэффициент вязкости, Па·с.
Твердообразные, вязко-пластичные массы имеют структурный режим движения, при котором скорость движения в тонком слое около стенки (градиентный слой) резко возрастает, в следующем, промежуточном слое увеличивается незначительно, а центральная часть потока (ядро) движется, испытывая незначительные деформации за счет ползучести или пластичности продукта. Движение «степенных» жидкостей аналогично, но в ядре потока в зависимости от индекса течения в большей или меньшей мере, существует градиент скорости.
Жидкообразные продукты могут иметь ламинарный или турбулентный режим движения, что определяется величиной критерия Рейнольдса. При ламинарном режиме (Re < 2320) жидкость движется в виде слоев, не перемешивающихся друг с другом. Однако для структурированных мясопродуктов (бульон, расплавленный жир и др.) ламинарный режим имеет место при Re < 1400. При турбулентном режиме происходит интенсивное внутреннее перемешивание жидкости. Однако у стенки сохраняется ламинарный слой, толщина которого с увеличением критерия Рейнольдса или скорости потока движения при прочих равных условиях уменьшается. Если толщина этого слоя больше высоты выступов шероховатости материала стенки, то трубы считаются гидравлически гладкими, в противном случае - шероховатыми.
Традиционная теория реодинамики исходит из гипотезы сплошности и непрерывности среды, и использует следующие допущения и ограничения:
- скорость движения жидкости на стенке принимается равной нулю, и продукт считается несжимаемым;
- реологические характеристики продукта неизменны по длине и не зависят от времени, т. е. на течение не влияют процессы тиксотропии, реопексии и релаксации.
Однако отмечены случаи проскальзывания продукта относительно стенки, т. е. скорость на стенке не равна нулю. Теория предусматривает, например, для степенных жидкостей при индексе течения, равном нулю, «стержневой» режим движения, при котором вся масса перемещается как твердый стержень и скорость движения на стенке равна среднеобъемной скорости потока, а градиент скорости на стенке стремится к бесконечности.
В последнее время в связи с требованиями практики и для получения боле точных данных пытаются учитывать изменения реологических характеристик (вязкости, плотности и др.) по длине трубы и во времени, рассматривая отклонение их величин последовательно по отдельным участкам длины трубы. Особую роль при этом играет постоянство градиента давления по длине трубы для некоторых, сжимаемых пластично-вязких продуктов.
Теория реодинамики для различных по своей текучести систем рассматривает равномерное (силы инерции равны нулю), прямолинейное (центробежные силы равны нулю) движение в горизонтальной трубе (силы тяжести проектируются на ось, совпадающую с направлением движения). В перемещаемой жидкости выделяется цилиндр радиусом 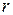 и длиной l, которой считается отвердевшим без изменения свойств. Условия такого движения цилиндра определяются исходя из равенства разности сил давления, приложенных к торцам, и силы вязкого сопротивления, возникающей на боковой поверхности цилиндра при его движении, т. е.
и длиной l, которой считается отвердевшим без изменения свойств. Условия такого движения цилиндра определяются исходя из равенства разности сил давления, приложенных к торцам, и силы вязкого сопротивления, возникающей на боковой поверхности цилиндра при его движении, т. е.
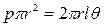 , (4.21)
, (4.21)
где р - разность давлений на торцах цилиндра; 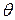 - касательное напряжение, создаваемое в продукте силой вязкого сопротивления.
- касательное напряжение, создаваемое в продукте силой вязкого сопротивления.
Решая уравнение (1) относительно 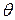 , получают выражение вида
, получают выражение вида
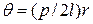 . (4.22)
. (4.22)
Из уравнения (5.6) видно, что напряжение на оси трубы (при r = 0) равно нулю, а на ее стенке 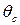 при радиусе r=R или диаметре d - наибольшее:
при радиусе r=R или диаметре d - наибольшее:
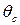 =(р/ 2 l) R= (р/ 4 l) d, (4.23)
=(р/ 2 l) R= (р/ 4 l) d, (4.23)
где R, d - соответственно радиус и диаметр трубы.
Сопоставляя выражения (4.22) и (4.23), получают уравнение для значения напряжения на любом расстоянии от оси трубы
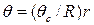 . (4.24)
. (4.24)
Истинный градиент скорости 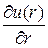 (где и (r) - скорость слоя радиусом r) представляют в виде функции напряжения сдвига
(где и (r) - скорость слоя радиусом r) представляют в виде функции напряжения сдвига 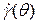 :
:
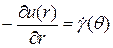 , (4.25)
, (4.25)
Знак «–» показывает, что скорость с увеличением радиуса уменьшается, поскольку начало отсчета производится от оси трубы. Интегрирование в пределах от r до R дает
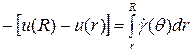 .
.
Проскальзывание отсутствует, поэтому и(R) = 0. Подача жидкости d 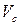 через элементарный слой радиусом r и толщиной dr с точностью до бесконечно малой второго порядка определяется в соответствии с уравнением расхода (подачи):
через элементарный слой радиусом r и толщиной dr с точностью до бесконечно малой второго порядка определяется в соответствии с уравнением расхода (подачи):
dV  = 2
= 2 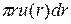
Для решения этого дифференциального уравнения интегрируют левую и правую части соответственно в пределах от 0 до V  и от 0 до R.
и от 0 до R.
Интеграл левой части равен V  , интеграл правой имеет вид:
, интеграл правой имеет вид: 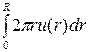 .
.
Обозначим  х = и (r); dy = 2
х = и (r); dy = 2 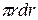 .
.
Тогда dx = [ dи (r)/ dr ] dr = 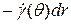 , у =
, у = 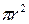 .
.
Далее, применяя правило интегрирования по частям и подставляя значения r= R и r= 0, получаем выражение вида
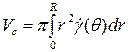 . (4.26)
. (4.26)
Из формулы (4.22) получаем r = 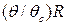 ;
; 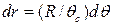 .
.
Тогда выражение (4.26) можно представить в самом общем виде
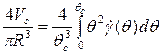 (4.27)
(4.27)
Полученное уравнение справедливо только в том случае, если закон изменения 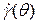 выражается одной непрерывной функцией. Если функция не непрерывна, то для каждого участка следует брать свой интеграл в соответствующих пределах. Например, по уравнению Шведова-Бингама ядро потока движется как твердый стержень, т. е. градиент скорости в нем равен нулю, и первый интеграл берут в пределах от 0 до
выражается одной непрерывной функцией. Если функция не непрерывна, то для каждого участка следует брать свой интеграл в соответствующих пределах. Например, по уравнению Шведова-Бингама ядро потока движется как твердый стержень, т. е. градиент скорости в нем равен нулю, и первый интеграл берут в пределах от 0 до 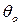 . В пристенном слое градиент не равен нулю, и второй интеграл имеет пределы от
. В пристенном слое градиент не равен нулю, и второй интеграл имеет пределы от 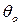 до
до 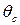 .
.
Ниже приведены результаты решения уравнения (4.27) относительно конкретных видов жидкостей и продуктов.
Для линейной ньютовской жидкости. Уравнение течения жидкости имеет вид:
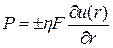 или
или 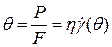 , (4.28)
, (4.28)
где Р - сила вязкого сопротивления; F - площадь боковой поверхности цилиндра радиусом r.
Из уравнения (4.28) 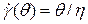 . Интегрируя уравнения (4.27), получают уравнение Пуазейля
. Интегрируя уравнения (4.27), получают уравнение Пуазейля
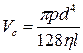 , или
, или 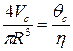 , или
, или 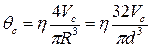 , (4.29)
, (4.29)
представляющее собой основной теоретический закон ламинарного потока ньютовской жидкости (используется и для неньютовских систем, тогда под понятием «вязкость» условно подразумевается эффективная вязкость или какой-либо другой ее эквивалент).
Расход (подача) и среднеобъемная скорость связаны соотношением, в результате получают
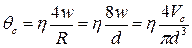 . (4.30)
. (4.30)
В этих выражениях по аналогии с законом вязкого сопротивления Ньютона находим консистентную переменную - «напряжение сдвига»
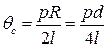 , (4.31)
, (4.31)
и консистентную переменную - «градиент скорости»
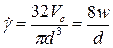 . (4.32)
. (4.32)
Из уравнения Пуазейля получают выражение определения вязкости жидкости
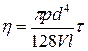 . (4.33)
. (4.33)
Для линейной системы Шведова-Бингама. Уравнение течения жидкости имеет вид:
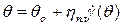 или
или 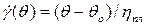 , (4.34)
, (4.34)
где 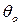 - предельное напряжение сдвига, Па;
- предельное напряжение сдвига, Па; 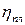 - пластическая вязкость, Па·с.
- пластическая вязкость, Па·с.
Подставляя последнее выражение в общее уравнение и интегрируя с учетом того, что, при 0 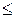 r
r 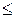
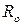 и 0
и 0 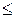
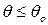 градиент скорости
градиент скорости 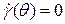 , получаем уравнение Букингама, которому после замены и подстановки придается вид, подобный уравнению Пуазейля:
, получаем уравнение Букингама, которому после замены и подстановки придается вид, подобный уравнению Пуазейля:
с 
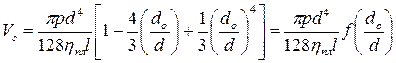 . (4.35)
. (4.35)
Запись этого уравнения в консистентных переменных имеет вид:
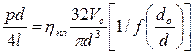 , (4.36)
, (4.36)
где 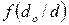 - функция ядра потока.
- функция ядра потока.
Ее значение и обратное значение принимаются из графиков.
Для нелинейной модели Кэссона. Уравнение течения жидкости имеет вид:
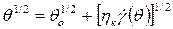 или
или 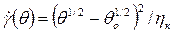 , (4.37)
, (4.37)
где 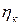 - вязкость по Кэссону, Па·с.
- вязкость по Кэссону, Па·с.
Выполнив аналогичные действия описанные выше получают уравнение вида уравнения Пуазейля:
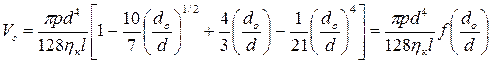 . (4.38)
. (4.38)
В консистентных переменных его записывают в следующем виде:
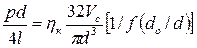 . (4.39)
. (4.39)
Анализ уравнений (5.19) и (5.22) показывает, что: при  d
d  = 0 (предельное напряжение сдвига отсутствует) жидкость течет как истинно вязкая по закону Пуазейля; при
= 0 (предельное напряжение сдвига отсутствует) жидкость течет как истинно вязкая по закону Пуазейля; при 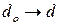 (т. е. при
(т. е. при 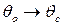 ) функция приближается к нулю и течение прекращается либо для обеспечения подачи давления стремится к бесконечности. Резкое увеличение давления для жидкости Кэссона начинается при
) функция приближается к нулю и течение прекращается либо для обеспечения подачи давления стремится к бесконечности. Резкое увеличение давления для жидкости Кэссона начинается при 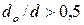 , для жидкости Бингама - при
, для жидкости Бингама - при 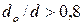 .
.
Для нелинейной степенной жидкости. Уравнение течения жидкости имеет вид:
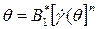 , (4.40)
, (4.40)
где 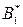 - коэффициент, пропорциональный вязкости, Па·с
- коэффициент, пропорциональный вязкости, Па·с 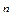 ; п - индекс течения.
; п - индекс течения.
В результате проведения математических действий получают уравнение общего вида:
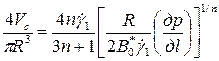 , (4.41)
, (4.41)
где 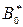 - коэффициент эффективной вязкости при единичном значении градиента скорости
- коэффициент эффективной вязкости при единичном значении градиента скорости 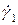 , не зависящем от напряжения; др/дl - градиент давления по длине трубы.
, не зависящем от напряжения; др/дl - градиент давления по длине трубы.
Данное уравнение в консистентных переменных имеет вид
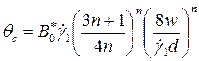 , (4.42)
, (4.42)
или
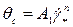 , (4.43)
, (4.43)
где А 1 - напряжение сдвига на стенке трубы при единичном значении относительного градиента скорости, Па; 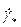 - относительный градиент скорости на стенке (консистентная переменная).
- относительный градиент скорости на стенке (консистентная переменная).
4.2 Расчеты трубопроводов и насадок для жидких, твердых и
вязко-пластичных пищевых масс
Расчет трубопроводов и насадок для жидкообразных продуктов.
К жидкообразным технологическим средам относят ряд мясопродуктов (бульон, расплавленный жир, кровь, сыворотку крови и т. д.), а также жидкие среды, обеспечивающие технологический процесс (рассол, воду, моющие и стерилизующие растворы и др.). Некоторые из перечисленных текучих сред являются ньютовскими жидкостями, другие могут в той или иной степени иметь аномалии вязкости. Поэтому значение общепринятого понятия «гидравлика» не будет соответствовать существу рассматриваемого вопроса. Его заменили термином «реодинамика», имеющим более универсальный смысл.
Основной задачей реодинамического расчета трубопровода является определение потерь давления или напора (энергии) в соответствующих сечениях трубы. Для большинства вышеперечисленных жидких сред общий энергетический баланс потока выражается уравнением Бернулли, которое для двух наиболее характерных сечений трубопровода имеет вид:
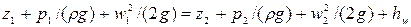 , (4.44)
, (4.44)
где 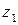 ,
, 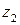 - геометрическая высота центров тяжести рассматриваемых сечений относительно горизонтальной плоскости сравнения, или удельная потенциальная энергия положения, м;
- геометрическая высота центров тяжести рассматриваемых сечений относительно горизонтальной плоскости сравнения, или удельная потенциальная энергия положения, м; 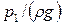 ,
, 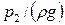 - пьезометрическая высота в рассматриваемых сечениях, или удельная потенциальная энергия давления, м;
- пьезометрическая высота в рассматриваемых сечениях, или удельная потенциальная энергия давления, м; 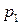 ,
, 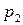 - давления в сечениях, Па;
- давления в сечениях, Па; 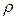 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3;  g - ускорение свободного падения, м/с2 (g =9,81 м/с2);
g - ускорение свободного падения, м/с2 (g =9,81 м/с2); 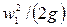 ,
, 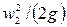 - скоростной напор в рассматриваемых сечениях, или удельная кинетическая энергия потока, м;
- скоростной напор в рассматриваемых сечениях, или удельная кинетическая энергия потока, м; 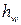 - потери энергии (напора) между этими сечениями, м.
- потери энергии (напора) между этими сечениями, м.
Потери давления адекватны удельным потерям энергии при течении жидкости, Они расходуются на преодоление сопротивлений движения по длине трубы и в местных сопротивлениях. Первые обусловлены внутренним и внешним трением в жидкости, вторые - изменением скорости по величине или направлению (краны, угольники, диафрагмы и пр.).
Потери давления и напора связаны соотношением: 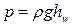 .
.
Общие потери напора определяют по формуле:
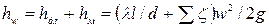 , (4.45)
, (4.45)
где 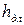 - потери напора по длине, м;
- потери напора по длине, м; 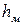 - потери напора в местных сопротивлениях, м;
- потери напора в местных сопротивлениях, м; 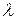 - коэффициент сопротивления трения по длине трубы; l - геометрическая длина трубопровода, м;
- коэффициент сопротивления трения по длине трубы; l - геометрическая длина трубопровода, м; 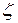 - коэффициент местного сопротивления.
- коэффициент местного сопротивления.
На одном трубопроводе может быть несколько местных сопротивлений: вход и выход из трубы, коленья, запорная арматура, поэтому величины коэффициентов суммируются.
Для определения потерь напора для прямых участков труб (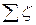 =0) используют первую водопроводную формулу Дарси-Вейсбаха:
=0) используют первую водопроводную формулу Дарси-Вейсбаха:
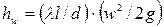 . (4.46)
. (4.46)
Для кольцевых, квадратных и тому подобных сечений вместо диаметра подставляют эквивалентный диаметр, определяемый по формуле:
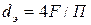 , (4.47)
, (4.47)
где 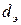 - эквивалентный диаметр, м; F - площадь живого сечения потока, м2; П - длина смоченного периметра, м.
- эквивалентный диаметр, м; F - площадь живого сечения потока, м2; П - длина смоченного периметра, м.
Для труб с местными сопротивлениями потери напора определяют по формуле:
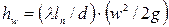 ,
,
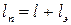 ; (4.48)
; (4.48)
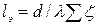 ,
,
где 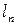 - приведенная длина трубопровода, м;
- приведенная длина трубопровода, м; 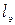 - эквивалентная длина, м (потери напора по длине эквивалентны потерям напора в местных сопротивлениях реального трубопровода).
- эквивалентная длина, м (потери напора по длине эквивалентны потерям напора в местных сопротивлениях реального трубопровода).
Наряду с формулами (5.30) и (5.32) потери напора определяют по видоизмененной первой водопроводной формуле:
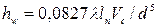 . (4.49)
. (4.49)
Для ориентировочного расчета потерь напора в длинных трубопроводах (потери напора в местных сопротивлениях составляют менее 20 % потерь напора по длине) потери напора в местных сопротивлениях не рассчитывают, а увеличивают значение потерь напора по длине на 20-30 %.
Таким образом, решение задач по расчету потерь напора при транспортировании жидкообразных мясопродуктов (формулы 5.30, 5.32, 5.33) сводится к определению коэффициентов сопротивления. Расчеты по их определению рассмотрены ниже.
В общей случае коэффициент сопротивления трения по длине трубы 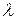 зависит от критерия Рейнольдса и относительной шероховатости трубы:
зависит от критерия Рейнольдса и относительной шероховатости трубы:
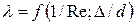 , (4.50)
, (4.50)
где 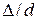 - относительная шероховатость трубы;
- относительная шероховатость трубы; 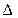 - абсолютная высота выступов шероховатости трубы, м.
- абсолютная высота выступов шероховатости трубы, м. 
Критерий Рейнольдса определяют по формуле:
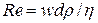 , (4.51)
, (4.51)
где 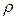 - плотность жидкости, кг/м3;
- плотность жидкости, кг/м3; 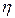 - вязкость жидкости, Па·с.
- вязкость жидкости, Па·с.
В гидравлически гладких трубах шероховатость практически не оказывает влияния на потери энергии, а в гидравлически шероховатых трубах происходит дополнительная турбулизация потока, и увеличиваются потери энергии.
Величину коэффициентов сопротивления при различных режимах движения жидкости определяют по графику Никурадзе (рис. 4.1)
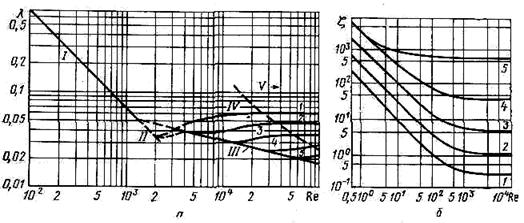
Рис. 4.1 Зависимость коэффициентов гидравлических сопротивлений
от критерия Рейнольдса:
а) - по длине трубы для различных зон движения жидкости
при различной относительной шероховатости трубы:
1 - 0,0334; 2 - 0,0164; 3 - 0,0083; 4 - 0,004; 5 - 0,0002; I - ламинарная зона движения жидкости;
II - переходная зона движения; Ш - турбулентная зона движения в гидравлически гладких трубах;
IV - турбулентная зона движения в шероховатых трубах;
V - автомодельная, или квадратичная, зона движения;
б) - в местных сопротивлениях:
1 - тройник; 2 – угольник 90о; 3 - открытый вентиль; 4 - шаровой кран; 5 - диафрагма (степень сжатия 0,05).
Для I зоны (ламинарный режим движения жидкости):
R е < 1400, 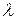 = К/Rе,
= К/Rе,
где К - коэффициент (для маловязких жидкостей К =64, высоковязких - К =70);
для II зоны (переход от ламинарного к турбулентному движению жидкости):
2000 < Rе < 5000, 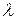 = 2,7/ Rе0,53;
= 2,7/ Rе0,53;
для III зоны (турбулентный режим движения в гидравлически гладких трубах):
5000 < Rе < 7000, 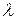 = 0,3164/ Rе0,25;
= 0,3164/ Rе0,25;
для IV зоны (турбулентное движение в шероховатых трубах):
2300 < Rе < 218 d/ 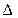 ,
, 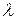 = 0,1
= 0,1 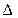 /d+ 100/ Rе0,25 или
/d+ 100/ Rе0,25 или 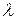 = 1,5/106 d0,3 +1/ Rе0,3;
= 1,5/106 d0,3 +1/ Rе0,3;
для V зоны (автомодельный, или квадратичный режим движения):
Rе > 125 d / 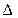 ,
, 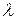 = 0,11
= 0,11 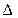 / d0,25.
/ d0,25.
Абсолютная величина выступов шероховатости зависит от вида перекачиваемой жидкости, материала трубы, длительности ее эксплуатации и их значения представлены в табл. 4.1.
Таблица 4.1
 2015-03-08
2015-03-08 2476
2476
