Полный расчет мембранных установок включает в себя технологический, гидравлический и механический расчеты. В ряде случаев, когда используют системы подогрева или охлаждения растворов, необходим также тепловой расчет. 3 ходе технологического расчета определяют необходимую поверхность мембран, жидкостные потоки и их состав. Цель гидравлического расчет а-определение гидравлического сопротивления аппаратов и арматуры, механического- обоснование размеров элементов аппаратов и выбор арматуры для работы установки при соответствующих давлениях. Тепловой рас чет позволяет определить необходимую поверхность теплопередачи и расход тепло- и хладоносителей.
Материальный баланс баромембранных процессов. Обычно мембранные процессы проводят при постоянных температуре и, явлении. Заданными величинами являются: количество исходного раствора L0 (кг/ч) и его состав с 0 (кг/кг), концентрация пермеата с2 (кг/кг), а также выход пермеата а:
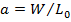 (24.12)
(24.12)
где W- расход пермеата, кг/ч.
По выходу пермеата а определяют его количество:
|
|
|
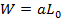 (24.13)
(24.13)
Материальный баланс по потокам
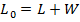 (24.14)
(24.14)
где L -расход ретанта (концентрата)
Из выражения (24.14) находят расход ретанта:
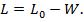 (24.15)
(24.15)
Материальный баланс по компоненту
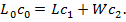 (24.16)
(24.16)
Тогда с учетом (24.15) состав ретанта
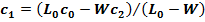 , (24.17)
, (24.17)
или
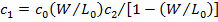 (24.18)
(24.18)
Полученные уравнения могут быть использованы и для расчета других мембранных процессов.
С учетом выражения (24.12) последнее уравнение примет следующий вид:
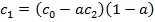 (24.19)
(24.19)
После этого определяют селективность φ мембраны с помощью выражения (24.1). По величине φ с учетом свойств разделяемого раствора по справочникам подбирают соответствующую марку мембраны. Затем для этой мембраны находят зависимость удельной производительности мембраны от состава разделяемого раствора лад мембраной:
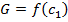 (24.20)
(24.20)
Зная величины G и с1, по выражению (24.2) с учетом выражения (24.13) находят поверхность F полупроницаемой мембраны:
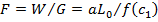 (24.21)
(24.21)
Расчет поверхности мембраны. Расчет проводят на основе уравнения массопередачи. Разработка методов расчета мембранных процессов и аппаратов непосредственно связана с анализом механизма процессов. При решении данной проблемы возможны различные подходы. Один подход состоит в том, чтобы на основе уравнений гидродинамики (Навье - Стокса и неразрывности потока) и массопереноса (конвективной и молекулярной диффузии) получить уравнения для определения основных технологических характеристик (селективности, проницаемости, требуемой поверхности мембран). Этот подход наиболее верен. Его стремятся использовать для решенья подобных задач применительно ко всем другим массообменным процессам, рассмотренным выше.
|
|
|
Однако эгот путь, как отмечалось ранее, оказывается очень сложным: трудно найти распределение концентраций в пограничных слоях фаз, часто затруднительно определить поверхность контакта фаз и т.д. Поэтому часто используют другой подход, широко применяемый в инженерных расчетах тепломассообменной аппаратуры: процесс разбивают на отдельные стадии, находят уравнения для определения скорости переноса на каждой стадии и по уравнению массопередачи рассчитывают необходимую поверхность массопереноса, в данном случае-рабочую поверхность мембраны. К достоинствам такого метода следует отнести прежде всего возможность получения обобщенных зависимостей для определения скоростей отдельных стадий процесса, что в конечном итоге позволяем рассчитывать мембранные аппараты без проведения предварительных экспериментов.
В общем случае количество вещества, проходящго через мембрану, можно определить по основному кинетическому уравнению массопередачи:
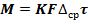 (24.22)
(24.22)
где К-коэффициент масссопередачи; F- рабочая поверхность мембраны: Аср-движущая сила мембранного разделения, τ – продолжительность процесса.
Из уравнения (24.22) получаем выражение для определения рабочей поверхности мембраны:
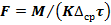 (24.22а)
(24.22а)
Если принять, что М - количество какого-либо компонента (или компонентов) смеси, переходящего через мембрану, то М можно определить из уравнения материального баланса (обычно допустимый перенос компонента разделяемой смеси через мембрану задается).
Коэффициент массопередачи К при переносе вещества через мембрану
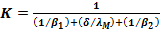 , (24.23)
, (24.23)
Где 𝛃1 коэффициент массоотдачи от потопа разделяемой смеси к поверхности мембраны. Δ - толшина мембраны; коэффициент массопроводности мембраны Р2 -коэффициент массоотдачи от мембраны в поток пермеата.
Коэффициент массопередачи К может быть выражен через общее сопротивление R переносу мембраны 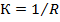 , причем
, причем
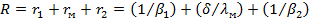 (24.4)
(24.4)
где 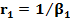 и
и 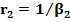 -сопротивление массопереносу соответственно со сторон разделяемой смеси и пермеата;
-сопротивление массопереносу соответственно со сторон разделяемой смеси и пермеата; 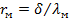 - сопротивление массопереносу в мембране.
- сопротивление массопереносу в мембране.
Вклад отдельных видов сопротивлений в общее (R) различен и зависит от типа мембранной о процесса и условий ею проведения. Например, при диффузионном разделении газов при условии небольшого перепада давлений через, мембрану основное сопротивление процессу сосредоточено в самой мембране (rM» r1 + r2), и со- противлениями r1 и r2 можно пренебречь,; при обратном осмосе и ультра фильтрации обычно пренебрежимо малой является величина г2; при испарении через мембрану могут быть соизмеримы все виды сопротивлений-r 1, rм и r2.
Наиболее сложным при использовании уравнения (24.22а) для расчета рабочей поверхности мембраны является определение значения rм. Поэтому для такой задачи приходится ставить эксперимент. Кроме того, для ряда мембранных процессов не всегда легко определить значение ∆ср. Поэтому расчет рабочей поверхности мембран на основе уравнения массопередачи нуждается в дальнейшей разработке.
Гидравлические и тепловые расчеты были рассмотрены в соответствуют их разделах данного учебника. Необходимые для таких расчетов справочные величины приведены в специальной литературе.
Особое место при расчете мембранных процессов занимает учет явления концентрированной поляризации.
Расчет концентрацнонной поляризации. В процессе разделения, например, жидких систем через мембрану проходит преимущественно растворитель. При этом концентрация растворенного вещества в пограничном слое у поверхности мембраны повышается. Повышение концентрации происходит до тех пор, пока диффузионный поток
растворенного вещества из пограничного слоя в разделяемый раствор не уравновесится потоком растворенного вещества через мембрану с установлением так называемого динамического равновесия.
|
|
|
Отношение концентрации раствореннлого вещества у поверхности мембраны к его концентрации в разделяемом растворе называют концентрационной поляризацией. Ее влияние на рабочие характеристики мембран отрицательно, так как вследствие увеличения осмотического давления раствора снижается движущая сила процесса разделения. Кроме того, при этом возможны выпадение в осадок и осаждение на мембране труднорастворимых солей, гелей высокомолекулярных соединений, что вызывает необходимость чистки или замены мембран.
Расчет концентрационной поляризации проводят, исходя из различных моделей процесса массопереноса растворенного вещест-
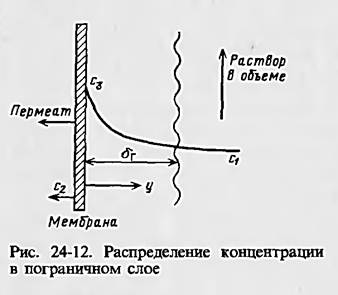
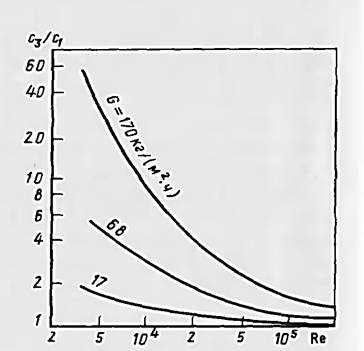
Рис.24-13. Концентрационная поляризация в турбулентном потоке
ва через мембрану. При использовании модели с распределением концентрации растворенного вещества у поверхности мембраны, показанным на рис. 24-12, предполагают, что растворенное вещество переносится в пограничном слое молекулярной диффузией и конвекцией. В этом случае
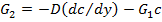 (24.25)
(24.25)
где G1 и G2 -удельная проницаемость мембраны соответсвенно по растворителю и растворенном у веществу; D -коэффициент диффузии растворенного вещества в растворе; с - концентрация растворенного вещества; у - расстояние от рассматриваемрй точки до поверхности мембраны. Введем понятие истинной селективности φи, т.е. селективности с учетом явления концентрационной поляризации:
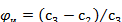 (24.26)
(24.26)
где c3-концентрация растворенного вещества у поверхности мембраны.
При допущении постоянства потока растворенного вещества по всей длине пограничного слоя
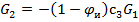 (24.27)
(24.27)
С учетом уравнений (24.26) и (24.27) получим
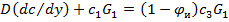 (24.28)
(24.28)
Гранитными условиями являются:
при у = 0 с = с3; при у = δг c=c1
где δг -толщина пограничного слоя.
Интегрируя уравнение (24.28), получим
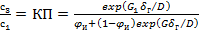 (24.29)
(24.29)
 2015-03-08
2015-03-08 2416
2416