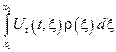Общее количество движения

– количество движений струны или работа, которую совершает струна в данный момент времени (на отрезке [ x ₁, x ₂]) → 1)

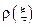– точечная плотность струны

1) Под воздействием силы натяжения и внешних сил

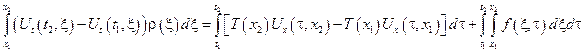– уравнение малых поперечных колебаний струны в интегральной форме, т.к. функция U (x, t) дважды непрерывно дифференцируема.

Т (х) – непрерывно дифференцируема.

По теории Лагранжа о конечных приращениях:

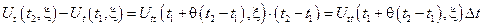
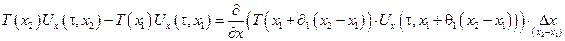
где 0 < (θ и θ₁) < 1.

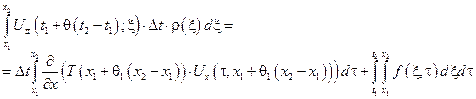
Воспользуемся теоремой о среднем значении для интеграла Римана

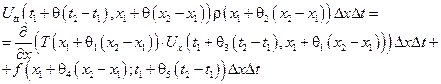
Разделим обе части равенства на 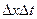и устремим t ₂ → t ₁, x ₂ → x ₁.

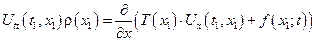
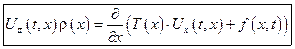
уравнение малых колебаний поперечной струны

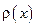– точечная плотность струны

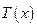– сила натяжения струны в т. х

В случае, когда ,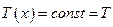

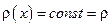
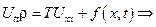
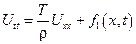, обозначим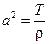

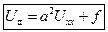уравнение малых поперечных колебаний струны.

Очевидно, что уравнение является квазилинейным

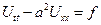
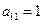
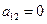
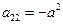
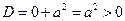– уравнение гиперболического типа и называется – одномерное волновое уравнение.