Случай 3
D < 0
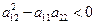 составим уравнение характеристик.
составим уравнение характеристик.
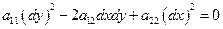
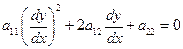
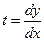
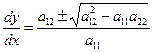
последнее уравнение имеет комплексное аналитическое решение
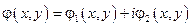 , где
, где
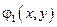 – действительная часть решения,
– действительная часть решения,
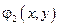 – мнимая часть решения.
– мнимая часть решения.
Замена:
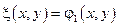
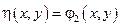
Можно показать, что
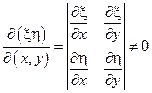
Функция 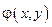 является решением уравнения
является решением уравнения
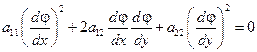
См. случай 2
Откуда получаем, что
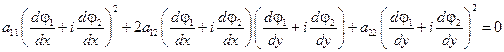
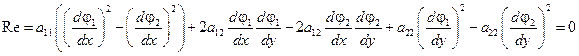
Откуда вытекает (см. случай 1) (выражение для коэффициентов 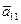 ,
, 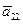
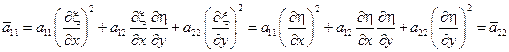
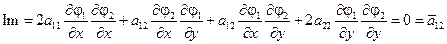
Следовательно, в новых переменных уравнение приобретает вид:
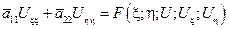
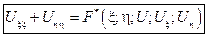 канонический вид уравнения эллиптического типа.
канонический вид уравнения эллиптического типа.
Пример:
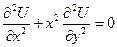 .
.
Решение:
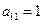
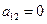
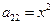
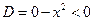 – уравнение эллиптического типа, если x ≠ 0.
– уравнение эллиптического типа, если x ≠ 0.
Уравнение характеристик
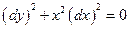
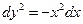
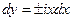
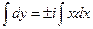
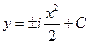 →
→ 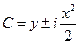
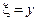
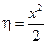
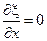
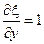
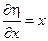
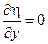
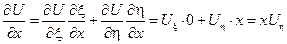
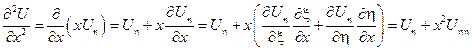
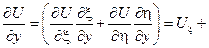
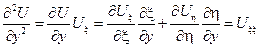
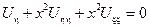
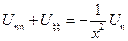
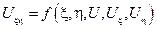
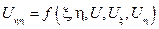
3. Эллиптические уравнения
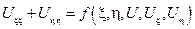
 2015-03-07
2015-03-07 4801
4801
