| Задача Коми | 1-ая краевая задача | 2-ая краевая задача |
1. 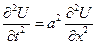 t >0
t >0 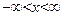 Однородная задача рассматр. струна бесконечная
U(x,0)=f(x) – условие задающее положение струны в начальный момент времени
Ut(x,0)=g(x) – скорость струны в начальный момент времени (нет воздействия внешних сил)
Однородная задача рассматр. струна бесконечная
U(x,0)=f(x) – условие задающее положение струны в начальный момент времени
Ut(x,0)=g(x) – скорость струны в начальный момент времени (нет воздействия внешних сил)
| 1. Однородная 1-ая краевая задача
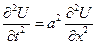 t >0
t >0 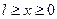 U(x,0)=f(x)
Начальное отклонение
Ut(x,0)=g(x) – начальная скорость
U(0,t)=μ(t) – закон. движение левого конца струны с течением времени
U(l,t)=μ2(t) – закон движения правого конца струны
U(x,0)=f(x)
Начальное отклонение
Ut(x,0)=g(x) – начальная скорость
U(0,t)=μ(t) – закон. движение левого конца струны с течением времени
U(l,t)=μ2(t) – закон движения правого конца струны
| 1. Однородная 2-ая краевая задача
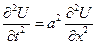 t >0
t >0 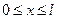 U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)=
U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)= 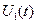 - сила действия на левый конец струны течением времени вдоль оси ОХ
Ux(l,t)= - сила действия на левый конец струны течением времени вдоль оси ОХ
Ux(l,t)= 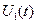 - сила действия на правый конец струны вдоль ОХ - сила действия на правый конец струны вдоль ОХ
|
2. Неоднородная задача
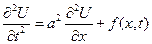 t >0
t >0 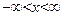 U(x,0)=f(x) – нач. положение
Ut(x,0)=g(x) есть воздействие внешних сил
U(x,0)=f(x) – нач. положение
Ut(x,0)=g(x) есть воздействие внешних сил
| 2. 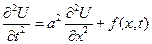 U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)=U(l,t)=0 - лев. и прав. концы закрепления
U(x,0)=f(x)
Ut(x,0)=g(x)
U(0,t)=U(l,t)=0 - лев. и прав. концы закрепления
| 2. Неоднородная задача
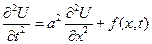 U(x,0)=f(x)
Ut(x,0)=g(x)
Ux(0,t)=Ux(l,t)=0 - вдоль оси концы не смещ. (однород. краев. услов. 2-ого типа
U(x,0)=f(x)
Ut(x,0)=g(x)
Ux(0,t)=Ux(l,t)=0 - вдоль оси концы не смещ. (однород. краев. услов. 2-ого типа
|
1,2 – первые краевые условия
Если U(0,t)=U(l,t)=0 – заданы 1-ые краевые условия однородные
3, 4 – краев. условия 2-ого типа для волнового уравнения
3-я задача краевого типа
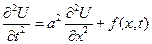 t >0
t >0 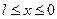
U(x,0)=f(x)
Ut(x,0)=g(x)
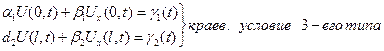
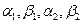 - заданные числа
- заданные числа
Краевые условии 1-ого типа описывают траектории движения левого и правого концов
Краевые условия 2-ого типа описывают силы, воздействующие на левый и правый концы, при этом в 1-ом случае не учитывается воздействие сил на концы, во 2-ом – не учитываются траектории их движения; краевые условия 3-его типа учитывают и то и другое.
 2015-03-07
2015-03-07 677
677








