1. Приведение одновременного волнового уравнения к канонической форме и его решение

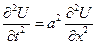
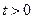
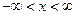
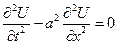
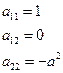
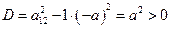 – уравнение гиперболического типа
– уравнение гиперболического типа
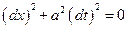
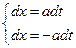
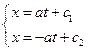
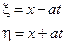
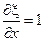
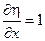
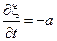
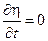
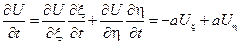
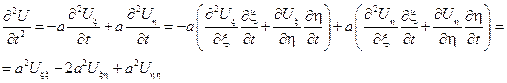
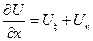
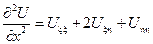
………
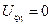
Общим решением полученного уравнения будет являться решение
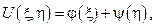 где
где
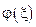 и
и 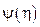 - любые дифференцируемые произвольные функции.
- любые дифференцируемые произвольные функции.
Заменяя ξ и η на их определение, получаем общее решение волнового уравнения в виде
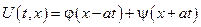
С физической точки зрения это решение интересно тем, что представляет собой сумму 2-х бегущих волн, движущихся в противоположных направлениях со скоростью а.
2. Решение Даламбера одномерного однородного волнового уравнения
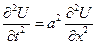
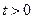
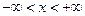
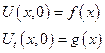
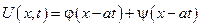 - определим функции φ и ψ однозначным образом, исходя из начальных условий
- определим функции φ и ψ однозначным образом, исходя из начальных условий
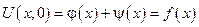
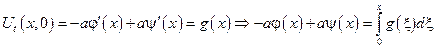
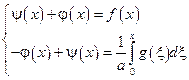
сложим: 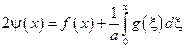
вычитаем: 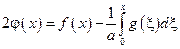
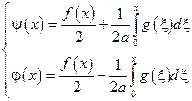
Подставим найденное выражение в общее решение исходного однородного уравнения:
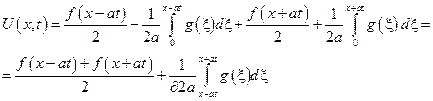
- решение однородной задачи Коши для бесконечной струны (формула Даламбера).
3. Неоднородная задача
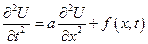
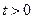
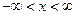
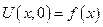
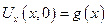
Будем искать решение в виде суммы 2-х функций.
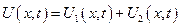
1) 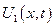 - решение однородной задачи
- решение однородной задачи
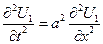
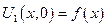
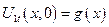
2) 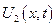 - решение неоднородной задачи с однородными краевыми условиями
- решение неоднородной задачи с однородными краевыми условиями
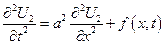
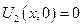
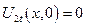
Решение 1-ой задачи – формула Даламбера
2-я задача решение:
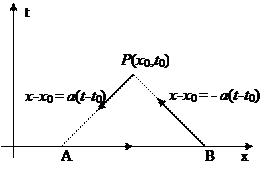
|
Уравнения прямой: 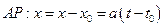
Уравнения прямой: 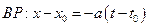
От обеих частей уравнения
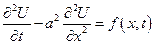 - возьмем интеграл по области R
- возьмем интеграл по области R
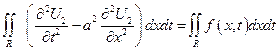
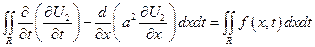
по формуле Грина (Стокса)
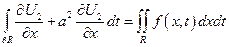
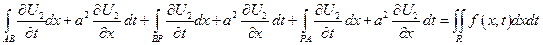
На 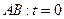
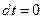
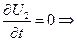
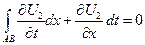
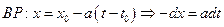
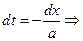
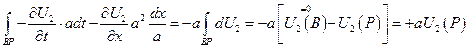
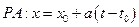
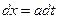
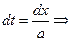
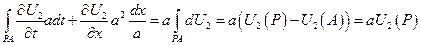
Подставляем в исходное уравнение
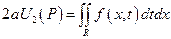 разделим на 2 а:
разделим на 2 а:
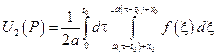
Следовательно, искомое решение неоднородного уравнения имеет вид: Римана – Вольтера
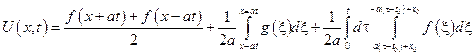
№8 Пример: Решить задачу Коши
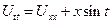
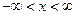
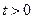
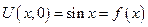
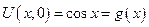
a = 1
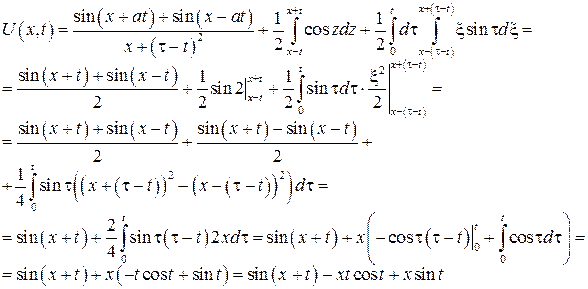
 2015-03-07
2015-03-07 2414
2414
