Интегральные уравнения встречаются в различных областях науки и многочисленных приложениях (в теории упругости, теории пластичности, гидродинамике, теории управления, химической технологии, биомеханике, теории массового обслуживания, экономике, медицине и др.)
Интегральные уравнения являются одним из наиболее плодотворных средств математического исследования как в чистом, так и в прикладном анализе. Это относится к задачам теории механических колебаний и соответствующих областей техники и теоретической физики, где интегральные уравнения не только полезны, но зачастую даже необходимы для численных расчетов.
Многие задачи математической физики приводят к линейным интегральным уравнениям.
Укажем некоторые типичные задачи, приводящие к таким уравнениям.
1.Равновесие нагруженной струны. Рассмотрим струну, т.е. некоторую материальную нить длины 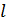 , которая может свободно изгибаться, но оказывает сопротивление растяжению, пропорциональное величине этого растяжения. Пусть концы закреплены в точках
, которая может свободно изгибаться, но оказывает сопротивление растяжению, пропорциональное величине этого растяжения. Пусть концы закреплены в точках 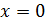 и
и 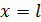 . Тогда в положении равновесия струна совпадает с отрезком оси
. Тогда в положении равновесия струна совпадает с отрезком оси 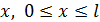 . Предположим теперь, что в точке
. Предположим теперь, что в точке 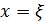 струны приложена вертикальная сила
струны приложена вертикальная сила 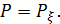 Под действием этой силы струна примет форму ломаной, изображенной на рисунке (1).
Под действием этой силы струна примет форму ломаной, изображенной на рисунке (1).
Найдем величину 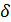 отклонения струны в точке
отклонения струны в точке 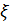 от положения равновесия под действием силы
от положения равновесия под действием силы 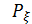 , приложенной в этой точке. Если сила
, приложенной в этой точке. Если сила 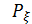 мала по сравнению с ненагруженной струны
мала по сравнению с ненагруженной струны 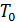 , то натяжение нагруженной струны можно по-прежнему считать равным
, то натяжение нагруженной струны можно по-прежнему считать равным 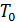 . Тогда, из условия равновесия струны получаем, такое равенство:
. Тогда, из условия равновесия струны получаем, такое равенство:
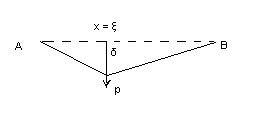 рис 1
рис 1
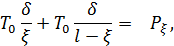
Откуда
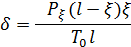
Пусть теперь 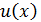 - прогиб струны в некоторой точке
- прогиб струны в некоторой точке 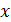 под действием силы
под действием силы 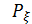 . Тогда
. Тогда
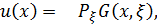
где 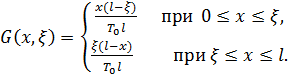
Из этих формул сразу видно, в частности, что 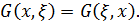
Предположим теперь, что струны действует сила, распределенная по ней непрерывно, с плотностью 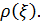 Если эта сила мала, то деформация зависит от силы линейно и форма нагруженной таким образом струны описывается функцией
Если эта сила мала, то деформация зависит от силы линейно и форма нагруженной таким образом струны описывается функцией
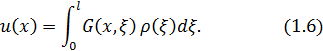
Итак, если задана нагрузка, действующая на струну, то по уравнению Вольтерра второго рода можно найти форму, которую примет струна под действием этой нагрузки.
Рассмотрим теперь обратную задачу: найти то распределение нагрузки 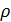 , при котором струна примет заданную форму
, при котором струна примет заданную форму 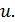 Мы получили для нахождения функции
Мы получили для нахождения функции 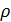 ,по заданной y, уравнение, которое с точностью до обозначений есть уравнение (1.1) т.е. интегральное уравнение Фредгольма первого рода.
,по заданной y, уравнение, которое с точностью до обозначений есть уравнение (1.1) т.е. интегральное уравнение Фредгольма первого рода.
2. Свободные и вынужденные колебания струны. Предположим теперь, что струна не находится в состоянии покоя, а совершает какие-то колебания. Пусть 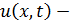 положение в момент
положение в момент 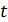 той точки струны, которая имеет абсциссу
той точки струны, которая имеет абсциссу 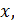 и пусть
и пусть 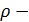 линейная плотность струны. Тогда на элемент струны длины
линейная плотность струны. Тогда на элемент струны длины 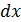 действует сила инерции, равная
действует сила инерции, равная
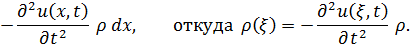
Подставив это выражение вместо 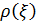 в формулу (1.6), мы получим
в формулу (1.6), мы получим
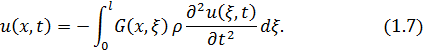
Предположим, что струна совершает гармонические колебания с некоторой фиксированной частотой 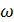 и амплитудой
и амплитудой 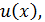 зависящий от
зависящий от 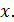
Иначе говоря, пусть
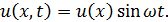
Подставив это выражение в (1.7) и разделив обе части равенства на 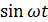 , получаем для
, получаем для 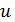 следующее интегральное уравнение:
следующее интегральное уравнение:
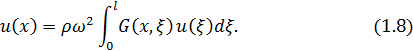
Если струна совершает не свободные колебания, а вынужденные, под действием внешней силы, то, как показывают несложные вычисления, соответствующее уравнений гармонических колебаний струны будет иметь вид
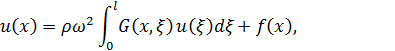
т.е. будет неоднородным уравнением Фредгольма второго рода.
2) Уравнения Вольтерра второго рода типичны при описании физических процессов, связанных с явлениями последствия. В этих уравнениях переменная x обычно обозначает время. Тогда состояние системы характеризуемое функцией 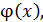 определяется внешним воздействием
определяется внешним воздействием 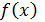 и зависит от состоянием системы в предшествующие моменты времени. Ядро
и зависит от состоянием системы в предшествующие моменты времени. Ядро 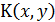 описывает величину последствия состояния системы в момент y на состояние системы в момент
описывает величину последствия состояния системы в момент y на состояние системы в момент 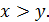
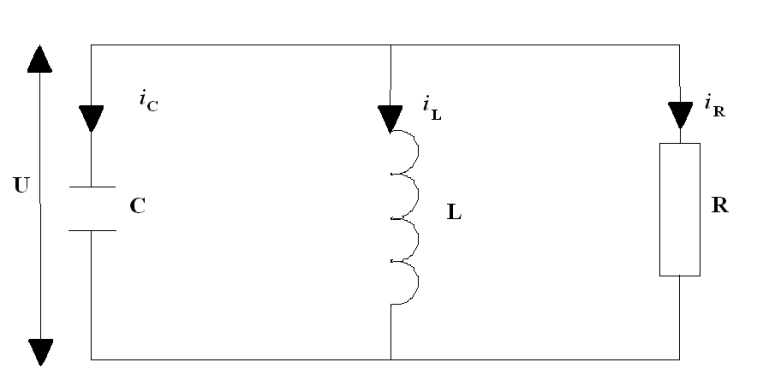 рис.2
рис.2
В качестве примера рассмотрим электрическую цепь, изображенную на рисунке 2. Пусть в катушке индуктивности не проявляется явлений гистерезиса. Тогда поток индукций в катушке 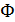 связан с током
связан с током 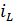 соотношением
соотношением 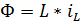 . Согласно известным формулам электродинамики имеем
. Согласно известным формулам электродинамики имеем
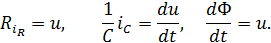
Используя закон Кирхгофа 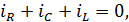 приходим к следующему дифференциальному уравнению относительно
приходим к следующему дифференциальному уравнению относительно 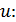
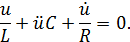
Пусть теперь катушка снабжена магнитным сердечником, в котором проявляется гистерезис. Тогда вместо соотношения 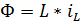 нужно использовать более сложное, учитывающее зависимость
нужно использовать более сложное, учитывающее зависимость 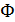 не только от значений
не только от значений 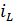 в момент времени t, но и в предшествующие моменты времени(эффект последствия). Это видоизмененное соотношение таково:
в момент времени t, но и в предшествующие моменты времени(эффект последствия). Это видоизмененное соотношение таково:
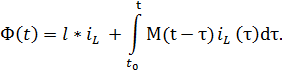
Здесь 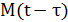 - функция, учитывающая влияние значения
- функция, учитывающая влияние значения 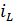 в момент времени
в момент времени  на величину
на величину 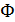 в момент времени
в момент времени 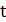 и определяемая эмпирическим способом.
и определяемая эмпирическим способом.
Имеем
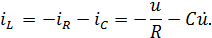
Отсюда
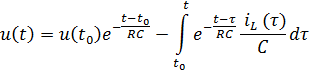
и следовательно,
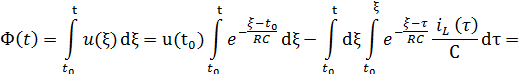
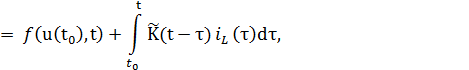
где
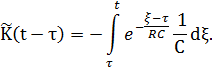
Подставляя полученное выражение для 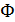 в уравнение, связывающее
в уравнение, связывающее 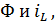
Получим
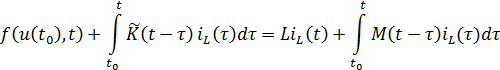
или, окончательно, для 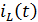 имеем
имеем
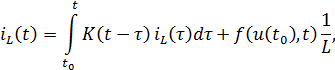
где 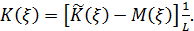
Таким образом, приходим к интегральному уравнению Вольтерра второго род
 2015-03-08
2015-03-08 899
899







