Методы и модели оптимизации портфеля ценных бумаг

Рассмотрим некоторые исходные положения, используемые при формировании и оптимизации портфеля ценных бумаг.

Первое из них состоит в том, что любой вид рисковых ценных бумаг можно охарактеризовать двумя величинами: ожидаемой эффективностью и мерой риска – вариацией или среднеквадратичным отклонением эффективности от ожидаемой. Эти же величины можно вычислить для любого портфеля ценных бумаг, если известны взаимосвязи между отдельными ценными бумагами и их эффективностью.

Второе – в том, что как ожидаемая эффективность портфеля, так и его рискованность будут зависеть от его структуры, то есть от доли исходного капитала, вложенной в каждый вид ценных бумаг.

При этом вполне естественным является желание инвестора одновременно обеспечить наибольшую эффективность портфеля и обеспечить вложение средств с наименьшим риском. Как известно, такое желание является противоречивым, поскольку, как правило, более прибыльные активы являются одновременно и более рискованными. Поэтому, для разрешения этого противоречия, при решении вопроса о том, какую долю капитала целесообразно вложить в каждый из циркулирующих на рынке видов ценных бумаг, приходится отыскивать оптимальное для данного инвестора соотношение доход-риск. Оптимизация такого портфеля по минимуму риска и максимуму получения экономической выгоды (отдачи) является одной из важнейших проблем инвестора.

Модель поведения инвестора, согласно которой инвестиции оцениваются исключительно по двум параметрам – ожидаемой доходности и риску, позволяет сформулировать единое правило формирования портфеля, которому следуют все без исключения инвесторы: независимо от индивидуальных предпочтений. Все инвесторы стремятся сформировать эффективный портфель – такой, который обеспечивает минимальную степень риска для выбранного уровня дохода, либо, что то же самое, максимальный ожидаемый доход при заданной степени риска. Как видим, здесь находит место проявление одно из правил теории и практики управления риском – правило оптимального сочетания выигрыша (отдачи) и величины риска. При этом, выбор заданной эффективности портфеля или заданной допустимой степени риска определяется самим инвестором. Этот выбор зависит от многих факторов – целей и задач, достижение которых решает инвестор при реализации инвестиционного проекта; политики, стратегии и тактики его инвестиционной деятельности; имущественного состояния инвестора, его воспитания, образования, социальных и психологических установок; склонности инвестора к риску и др.

Математическая формализация изложенного выше подхода к формированию эффективного портфеля ценных бумаг впервые была предложена американским ученым-экономистом Г. Марковицем (H. Markovitz). Этот подход, и сама задача, выбора эффективного портфеля носит название модели Марковица. О важности этой проблемы для экономической науки и практики свидетельствует тот факт, что за эту работу Г. Марковицу впоследствии была присуждена Нобелевская премия по экономике.

Модель Марковица в самом простейшем виде можно сформулировать следующим образом:

имеется 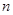видов ценных бумаг, которые может приобрести инвестор;

по каждому виду ценных бумаг известны: ожидаемая эффективность, вариация или среднеквадратическое отклонение эффективности от ожидаемой, а также взаимосвязи между отдельными ценными бумагами и их эффективностью;

необходимо найти такие пропорции распределения имеющихся средств между доступными активами: 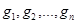(где 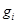- доля средств, инвестируемых в i-й актив), чтобы риск портфеля 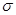при заданном уровне доходности 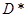был бы минимальным. Математически модель можно сформулировать так:

найти

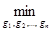
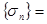
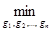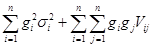{ }, (9.13)

при ограничениях

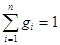, (9.14)

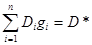, (9.15)

где 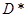- заданный уровень ожидаемой (средней) доходности портфеля.

В результате решения задачи будут получены численные значения доли средств 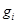, инвестируемых в каждый вид ценных бумаг. Значение 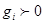, означает рекомендацию вложить долю 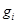наличного капитала в ценные бумаги вида 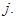Значение 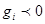означает рекомендацию взять в долг ценные бумаги этого вида в количестве - 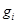(на единицу наличного капитала), то есть участвовать в операции типа short sale. Если такое невозможно, то в модель 9.13 – 9.15 следует ввести дополнительное ограничение – не отрицательности переменных ( 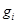³ 0).

В общем случае можно рассматривать бесчисленное множество ценных бумаг. При этом, в процессе решения задачи неэффективные бумаги будут исключены из портфеля. Для таких активов доля инвестируемых средств в результате решения задачи будет равной нулю.

Одной из сложностей практической реализации этой модели является подготовка исходной информации. Так, если для включения в портфель рассматриваются 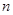финансовых активов, то для расчета стандартного отклонения доходности портфеля необходимо оценить 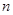показателей стандартного отклонения доходности каждого актива и 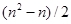показателей ковариации. Этот недостаток, в определенной мере, устранен в процессе дальнейшего развития портфельной теории.

Одним из направлений такого развития является разработка модели оценки капитальных активов (МОКА). В отличие от модели Марковица, которая рассматривает закономерности формирования индивидуальных инвестиционных решений, модель МОКА дополняет их характеристиками рынка в целом.

Модель МОКА. Основные допущения модели МОКА состоят в следующем:

- все инвесторы не склонны к риску и оценивают финансовые активы исключительно по двум параметрам – среднему (ожидаемому) доходу на единицу вложений и стандартному (среднеквадратическому) отклонению доходности, которое характеризует риск инвестирования;

- все инвесторы имеют равный доступ к информации и одинаково оценивают доходность и риск каждого актива;

- существует безрисковая ставка доходности 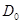, и все инвесторы имеют одинаковые и неограниченные возможности, как инвестирования, так и кредитования по данной процентной ставке;

- все активы могу делиться бесконечно, то есть имеется возможность приобретения и продажи активов любого количества.

В соответствии с основными положениями модели МОКА, доходность любой ценной бумаги, представленной на рынке, определяется следующими составляющими:

- безрисковой ставкой доходности ;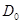

- доходностью рыночного портфеля ;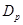

- риском (стандартным отклонением доходности) рыночного портфеля ;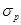

- ковариацией показателей доходности 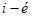ценной бумаги и доходности рыночного портфеля .

Все перечисленные составляющие, за исключением последней, одинаковые для всех ценных бумаг. Поэтому, в соответствии с моделью МОКА, отличие в доходности ценных бумаг определяется только величиной , которая рассматривается здесь как показатель риска ценной бумаги.

На практике, в качестве характеристики риска часто используется показатель , нормированный по величине дисперсии доходности рыночного портфеля 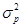, который называют бета коэффициентом 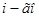актива = .

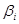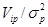Содержание, порядок расчета и использование бета коэффициента рассмотрено нами в разделе 4.4 данной книги. Как отмечалось, в большинстве случаев этот показатель применяется при принятии решений о вложении инвестиций в ценные бумаги и характеризует неустойчивость доходов по каждому виду ценных бумаг относительно доходов по "среднему" полностью диверсифицированному портфелю ценных бумаг, за который может быть принят весь рынок ценных бумаг.

Зависимость доходности 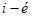ценной бумаги от величины бета коэффициента имеет следующий вид: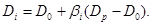

Представленное выражение можно рассматривать как зависимость между ожидаемой доходностью 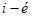ценной бумаги 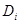и ожидаемой доходностью рыночного портфеля 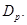Для случайной величины доходности 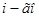актива 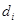можно записать:

,

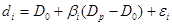где 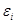- случайная величина, характеризующая отклонение 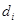от своего среднего значения.

Очевидно, что среднее значение этой случайной величины 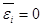, а ее дисперсию обозначим .

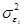В случае независимости случайных величин, получим: .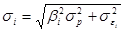

Используя свойства ковариации, для среднеквадратического отклонения доходности портфеля 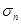можно записать:

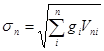, где 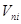- ковариация доходности портфеля и 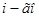актива.

Такое же соотношение справедливо и для рыночного портфеля:

.

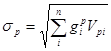Используя приведенные выше зависимости можно записать, что риск (среднеквадратическое отклонение доходности) любого портфеля будет равным

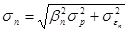. (9.16)

При этом 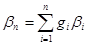, и при условии взаимной независимости величин : .

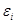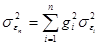В формуле 9.16, характеризующей риск портфеля, выражение 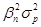характеризует рыночный, или систематический риск портфеля ценных бумаг, а 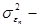остаточный, или индивидуальный (несистематический) риск.

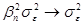В случае, когда структура любого портфеля приближается к структуре рыночного портфеля, величина , и, как следствие, . Одновременно .

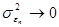Полученные таким образом результаты в рамках модели МОКА интерпретируются следующим образом.

Факторы, влияющие на цену и доходность любой ценной бумаги можно разделить на две основные категории:

- первая – это, так называемые, системные или общерыночные факторы, которые влияют на состояние экономики в целом. Эти факторы находят отражение в ценах и доходности всех ценных бумаг, которые обращаются на рынке и, соответственно, являются источником систематического (рыночного) риска;

- вторая – индивидуальные факторы, которые влияют на доходность каждого отдельного вида ценных бумаг, и являются источником остаточного или индивидуального (несистематического) риска.

Использование результатов и зависимостей, полученных в модели МОКА, позволило другому ученому-экономисту Шарпу, упростить задачу формирования оптимального портфеля ценных бумаг.

Воспользовавшись приведенной выше формулой 9.16 для расчета стандартного отклонения доходности портфеля, а также полученными выражениям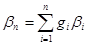и , и 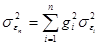, выражение для определения дисперсии доходности портфеля можно записать следующим образом:

.

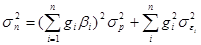Тогда модель Шарпа, которая отличается от модели Марковица только внешним видом целевой функции, можно описать следующим видом:

найти

.

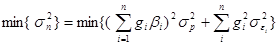при ограничениях

,

,

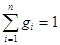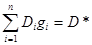где 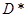- заданный уровень ожидаемой (средней) доходности портфеля.

Использование этой модели позволяет значительно облегчить подготовку исходной информации, необходимой для решения задачи нахождения оптимального портфеля ценных бумаг, поскольку количество параметров, которые необходимо определить вне рамок модели, уменьшается до 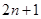. Так, например, если рассматриваются 100 видов ценных бумаг, количество статистических параметров, которые следует определить, для использования модели Марковица составляет 4950 единиц. В то время как для решения задачи с использованием модели Шарпа это число сокращается до 201 параметра.

Более подробное описание и примеры численного решения задачи формирования оптимального портфеля ценных бумаг можно найти в [41].

Следует отметить, что сложность решения задач управления риском, а также широкое распространение компьютерной техники, способствовали созданию разнообразного программного обеспечения, направленного на автоматизацию процесса решения этих задач. В частности, в [41] приведено описание пакета прикладных программ SAOF, который позволяет в автоматическом режиме решать задачи выбора оптимального портфеля ценных бумаг и подготавливать для них необходимую исходную информацию.

В следующем разделе будет приведена информация о некоторых из программных продуктов, используемых для автоматизации решения задач управления риском в различных сферах предпринимательской деятельности.