1) Из уравнений (2.1) можно прийти к уравнению (2.3) следующим образом: в качестве направляющего вектора прямой берём 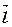 =[
=[ 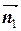 ,
, 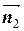 ] (векторное произведение векторов
] (векторное произведение векторов 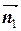 и
и 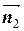 ), где
), где 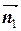 и
и 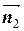 - нормали соответственно П 1 и П 2, а в качестве точки N (x 0, y 0, z 0) - некоторое частное решение системы (2.1). Обратный переход от (2.3) к (2.1) получаем сразу:
- нормали соответственно П 1 и П 2, а в качестве точки N (x 0, y 0, z 0) - некоторое частное решение системы (2.1). Обратный переход от (2.3) к (2.1) получаем сразу:
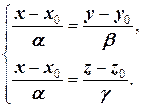
2) Как и в случае прямой на плоскости, в каноническом уравнении допускается, чтобы хотя бы один из параметров в знаменателе (но не все три одновременно) равнялся нулю.
3) если прямая проходит через точки N (x 0, y 0, z 0) и M (x 1, y 1, z 1), то каноническое уравнение записывается в виде
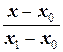 =
= 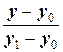 =
= 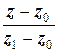 . (2.4)
. (2.4)
Уравнение (2.4) также называется уравнением прямой, проходящей через две точки.
 2015-03-08
2015-03-08 471
471








