2.1. Понятие линейной зависимости. Пусть V – линейное пространство над R,{ a 1, a 2, …, an } – произвольное множество векторов из V, a 1, a 2, …, ak - некоторые числа.
2.1.1. Определение. Выражение
a 1 a 1+ a 2 a 2+…+ akak (2.1.1)
называется линейной комбинацией векторов a 1, a 2, …, ak. При этом a 1, a 2, …, ak - коэффициенты соответственно приa 1, a 2, …, an.
Например, если a 1= 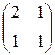 , a 2=
, a 2= 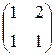 , a 3=
, a 3= 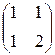 , a 4=
, a 4= 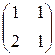 , то в силу
, то в силу
a 1 a 1+ a 2 a 2+ a 3 a 3+ a 4 a 4= a 1 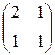 + a 2
+ a 2 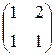 + a 3
+ a 3 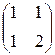 + a 4
+ a 4 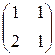 =
=
= 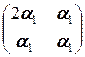 +
+ 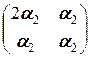 +
+ 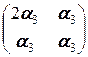 +
+ 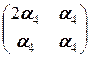 =
=
= 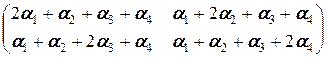
их линейной комбинацией является матрица
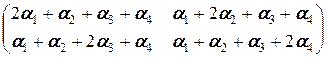 .
.
2.1.2. Определение. Система векторов
a 1, a 2, …, ak (2.1.2)
называется линейно независимой, если из того, что
a 1 a 1+ a 2 a 2+…+ akak =0 V (2.1.3)
следует α 1= α 2=…= αk =0. В противном случае, система (2.1.2) называется линейно зависимой. Другими словами
2.1.3. Определение. Система векторов (2.1.2) называется линейно зависимой если равенство (2.1.3) возможно при некоторых, не всех равных нулю, a 1, a 2, …, ak (или, другими словами, если существуют не все равные нулю a 1, a 2, …, ak такие, что выполняется равенство (2.1.3)).
Например, система векторов a 1= 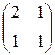 , a 2=
, a 2= 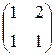 , a 3=
, a 3= 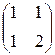 , a 4=
, a 4= 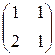 (линейного пространства M 2´2(R)) является линейно независимой, а система a 1=
(линейного пространства M 2´2(R)) является линейно независимой, а система a 1= 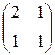 , a 2=
, a 2= 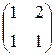 , a 3=
, a 3= 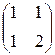 , a 4=
, a 4= 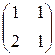 , a 5=
, a 5= 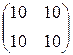 - линейно зависимая.
- линейно зависимая.
Действительно, составим для a 1, a 2, a 3, a 4 равенство (2.1.3): a 1 a 1+ a 2 a 2+ a 3 a 3+ a 4 a 4=0 V. Оно равносильно равенству
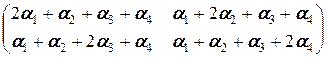 =
= 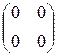 , (2.1.4)
, (2.1.4)
(в силу выписанной выше линейной комбинации матриц a 1, a 2, a 3, a 4). Равенство (2.1.4) равносильно системе уравнений
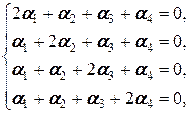
которая в свою очередь равносильна системе
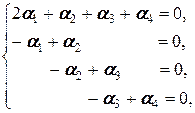
(первое уравнение вычли из второго, второе - из третьего, третье - из четвёртого), откуда a 1= a 2, a 2= a 3, a 3= a 4, то есть a 1= a 2= a 3= a 4, подставляя которое в первое уравнение, получаем 5 a 1=0, то есть a 1=0. Но тогда a 1= a 2= a 3= a 4=0, и матрицы a 1, a 2, a 3, a 4 (векторы в M 2´2(R)) линейно независимы.
Для доказательства линейной зависимости векторов a 1= 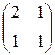 , a 2=
, a 2= 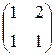 , a 3=
, a 3= 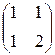 , a 4=
, a 4= 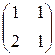 , a 5=
, a 5= 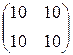 составим для них равенство (2.1.3): a 1 a 1+ a 2 a 2+ a 3 a 3+ a 4 a 4+ a 5 a 5=0 V, которое приводит к аналогу равенства (2.1.4):
составим для них равенство (2.1.3): a 1 a 1+ a 2 a 2+ a 3 a 3+ a 4 a 4+ a 5 a 5=0 V, которое приводит к аналогу равенства (2.1.4):
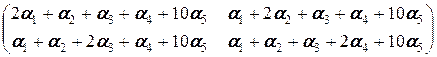 =
= 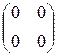 ,
,
равносильного системе
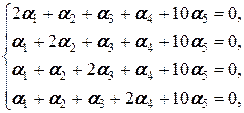
которая в свою очередь равносильна системе
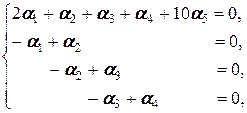
(снова первое уравнение вычли из второго, второе - из третьего, третье - из четвёртого), откуда a 1= a 2, a 2= a 3, a 3= a 4, то есть a 1= a 2= a 3= a 4, подставляя которое в первое уравнение, получаем 5 a 1+10 a 5=0, то есть a 1=-2 a 5. Положим a 5=1. Тогда a 1= a 2= a 3= a 4=-2, и равенство (2.1.3) для a 1, a 2, a 3, a 4, a 5 принимает вид -2 a 1-2 a 2-2 a 3-2 a 4+ a 5=0 V. Это означает, что a 1, a 2, a 3, a 4, a 5 линейно зависимы (существуют не все равные нулю a 1, a 2, a 3, a 4, a 5; точнее, ни один коэффициент при ai (i =1, 2, 3, 4, 5) не равен нулю).
2.1.4. Определение. Выражение (2.1.3) называется линейной зависимостью между векторами a 1, a 2, …, ak. Найти зависимость между векторамиa 1, a 2, …, ak - это значит найти a 1, a 2, …, ak, не все равные нулю, в выражении (2.1.3).
Так, -2 a 1-2 a 2-2 a 3-2 a 4+ a 5=0 V - линейная зависимость между векторами a 1= 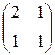 , a 2=
, a 2= 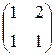 , a 3=
, a 3= 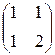 , a 4=
, a 4= 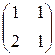 , a 5=
, a 5= 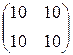 .
.
2.2. Простейшие свойства линейной зависимости.
2.2.1. Теорема ( о простейших свойствах линейной зависимости ). Линейная зависимость векторов обладает следующими свойствами:
1º. Система из одного ненулевого вектора линейно независима.
2º. Система векторов, содержащая нулевой, линейно зависима.
3º. Система векторов линейно зависима тогда и только тогда, когда некоторый вектор этой системы является линейной комбинацией остальных.
Именно, если a 1, a 2, …, ak линейно зависимы, то существуют не все равные нулю числа a 1, a 2, …, ak такие, что имеет место равенство (2.1.3). Тогда те векторы ai, коэффициенты при которых не равны нулю (ai ≠0), являются линейными комбинациями остальных. Например, если a 1≠0, то a 1= 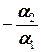 a 2
a 2 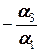 a 3-…
a 3-… 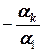 ak, то есть a 1 является линейной комбинацией остальных векторов a 2, a 3, …, ak.
ak, то есть a 1 является линейной комбинацией остальных векторов a 2, a 3, …, ak.
Так, для векторов a 1= 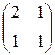 , a 2=
, a 2= 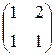 , a 3=
, a 3= 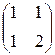 , a 4=
, a 4= 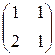 , a 5=
, a 5= 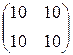 имеем a 5=2 a 1+2 a 2+2 a 3+2 a 4, или a 1=- a 2- a 3- a 4
имеем a 5=2 a 1+2 a 2+2 a 3+2 a 4, или a 1=- a 2- a 3- a 4 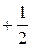 a 5, и, вообще, ai =- ak - al - am
a 5, и, вообще, ai =- ak - al - am 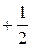 a 5, где { i, k, l, m }={1, 2, 3, 4}.
a 5, где { i, k, l, m }={1, 2, 3, 4}.
 2015-03-08
2015-03-08 1864
1864
