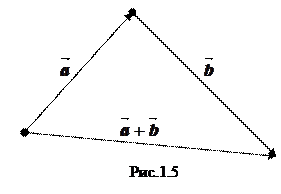 1.2.1. Суммой векторов
1.2.1. Суммой векторов  и
и 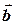 называется вектор, начало которого совпадает с началом
называется вектор, начало которого совпадает с началом  , а конец - с концом
, а конец - с концом  , при условии, что начало
, при условии, что начало  приложено к концу
приложено к концу  . Обозначается сумма
. Обозначается сумма  и
и  через
через  +
+  (рис.1.5).
(рис.1.5).
1.2.2. Теорема. Сумма векторов обладает следующими свойствами:
1о. Для любых векторов  и
и 
 +
+  =
=  +
+  .
.
2о. Для любых векторов  ,
,  и
и 
( +
+  )+
)+  =
=  +(
+( +
+  ).
).
3о. Существует такой вектор 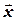 , что для любого вектора
, что для любого вектора 
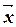 +
+  =
=  .
.
4о. Для любого вектора  существует вектор
существует вектор  такой, что
такой, что
 +
+  =
=  .
.
Прокомментируем перечисленные свойства.
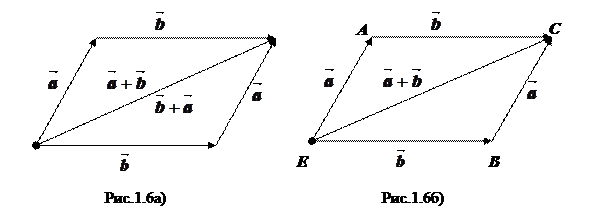
1о. Равенство векторов  +
+  и
и  +
+  усматривается из простых геометрических соображений, приведённых на рис.1.6а).
усматривается из простых геометрических соображений, приведённых на рис.1.6а).
Из этого свойства легко усматривается правило построения суммы векторов  и
и  : Для получения суммы
: Для получения суммы  +
+  достаточно отложить векторы
достаточно отложить векторы  и
и  из одной точки, построить параллелограмм EACB, где
из одной точки, построить параллелограмм EACB, где 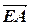 =
=  ,
, 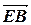 =
=  . Тогда
. Тогда 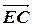 =
=  +
+  (рис.1.6б)). При этом говорят, что параллелограммEACBпостроен на векторах
(рис.1.6б)). При этом говорят, что параллелограммEACBпостроен на векторах  и
и  .
.
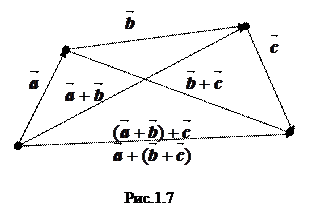 2о. Равенство векторов (
2о. Равенство векторов ( +
+  )+
)+  и
и  +(
+( +
+  ) также усматривается из геометрических соображений (рис.1.7).
) также усматривается из геометрических соображений (рис.1.7).
3о. Ясно, что роль 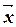 играет
играет  :
: 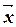 +
+  =
=  .
.
4о. В этом свойстве утверждается, что для любого вектора  существует противоположный -
существует противоположный -  : если
: если  =
=  , то
, то  =-
=-  =
= 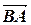 и
и  +
+ 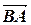 =
= 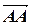 =
=  .
.
 2015-03-08
2015-03-08 652
652








