Множество векторов как линейное пространство

2.1.1. Теорема. Множество векторов на плоскости (в пространстве) образует линейное пространство.

Это вытекает из определения суммы векторов и произведения вектора на число, и из свойств этих операций. А именно, Теорема 1.2.2 даёт свойства 1^о - 4^о определения линейного пространства, а Теорема 1.3.2 - свойства 5^о - 8^о определения. Причём можно рассматривать (как линейное пространство) отдельно векторы на плоскости и отдельно в пространстве.

Из теоремы 2.1.1 вытекает, что для векторов (как на плоскости, так и в пространстве) выполнены все свойства линейного пространства (рассмотренные в главе I). Перечислим некоторые из них применительно к векторам:

1. Нулевой нулевой вектор единствен.

2. Для любого вектора его противоположный вектор - единствен.

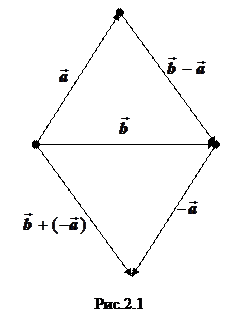3. Сумма вида (...(( 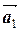+ 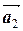)+ )+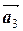...)+ 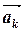не зависит от расстановки скобок. Поэтому скобки принято опускать: + +...+ .

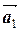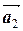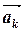4. Для любого вектора

-(- )= .

5. Для любых векторов , уравнения x + = и + x = имеют единственное решение x = +(- ). Это решение - разность векторов и : x = - .

Правило построения разности векторов и вытекает из рис.2.1:

Для построения вектора - достаточно отложить векторы и из одной точки. Тогда вектор - - вектор, начало которого совпадает с концом вектора , а конец - с концом вектора .

6. Для любых векторов , ,...,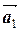

-( + +...+ )=- - -...- .

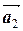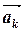
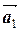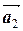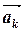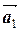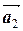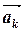7. Для любого вектора имеет место равенство 0 = .

8. Для любого числа a имеет место равенство a = .

9. Если a = , то либо a =0, либо = .

10. Для любого вектора и любого числа a имеет место равенство (- a) = -(a ), в частности, (-1) = - .

11. Для любых чисел a, a ₁, a ₂, …, a_k и любых векторов , , 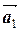,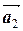..., 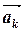имеют место равенства

(± a ₁± a ₂±…± a_k) =± a ₁ ± a ₂ ±…± a_k

и

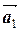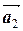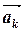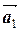a (± ± ±…± )=± a 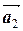± a ±…± a .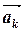

Также, на множество векторов (как на плоскости, так и в пространстве) переносятся все понятия линейного пространства (например, линейная комбинация векторов, линейная зависимость (независимость) векторов и их свойства, базис и.т.д.).

2.1.2. Теорема. На плоскости максимальное число линейно независимых векторов равно 2, в пространстве - 3. Любые k векторов, k >3 на плоскости и k >4 в пространстве, линейно независимы.

2.1.3. Теорема. На плоскости базис образует любая пара неколлинеарных векторов. В пространстве базис образует любая тройка некомпланарных векторов.

Таким образом, размерность линейного пространства геометрических векторов на плоскости равна 2, в пространстве - 3. Это означает, что в любом базисе на плоскости вектор имеет две координаты: =(a_x, a_y). В пространстве в любом базисе вектор имеет 3 координаты: =(a_x, a_y, a_z). При этом, напоминаем:

2.1.4. Теорема. Если =(a_x, a_y), =(b_x, b_y), a - произвольное число, то + =(a_x + b_x, a_y + b_y) и a =(aa_x, aa_y). В частности, - =(a_x - b_x, a_y - b_y)

Аналогичное свойство справедливо для векторов в пространстве.

Кроме того

2.1.5. Теорема. Два вектора и линейно зависимы тогда и только тогда, когда они коллинеарны, что равносильно пропорциональности их координат:

= a Û 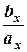= 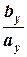(= a) - на плоскости

= a Û 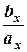= = 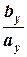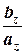(= a) - в пространстве

Три вектора , и линейно зависимы тогда и только тогда, когда они компланарны, что равносильно

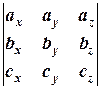=0.