Умножение вектора на число

1.3.1. Произведением (умножением) вектора на число a называется такой вектор , что:

1) | |=| a || |;

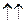
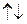
2) Если a >0, то , а если a <0, то (если a =0, то из условия 1) вытекает, что | |=0, то есть = ).

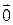Например, на рис.1.8 изображены векторы , 3 и .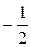

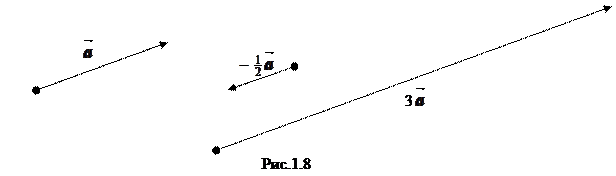
1.3.2. Теорема. Произведение вектора на число обладает следующими свойствами:

1^о. Для любого вектора

1 = .

2^о. Для любых чисел a, b и любого вектора

a (b )=(ab) .

3^о. Для любых чисел a, b и любого вектора

(a + b) = a + b .

4^о. Для любых числа a и векторов и

a ( + )= a + a .

Множество векторов как линейное пространство