1.1.1. Определение. Линейным уравнением с n неизвестными называется равенство вида
a 1 x 1+ a 2 x 2+…+ anxn = b, ( 1.1.1 )
где a 1 x 1+ a 2 x 2+…+ anxn ¾ многочлен от переменных x 1, x 2, …, xn. Переменные x 1, x 2, …, xn называются неизвестными уравнения (1.1.1), числа ai (i =1, …, n) ¾ коэффициентамипри неизвестныхxi (i =1, …, n) соответственно, b ¾ свободным членом.
Решением уравнения (1.1.1) называется любой упорядоченный набор (a 1, a 2, …, an) чисел ai (i =1, …, n), при подстановке которых соответственно вместо x 1, x 2, …, xn уравнение (1.1.1) обращается в верное числовое равенство: a 1 a 1+ a 2 a 2+…+ anan = b.
Решить уравнение (1.1.1) ¾ это значит найти множество всех его решений.
1.1.2. Упражнение. Решить уравнения:
а) 4 x 1-6 x 2=7;
б) 2 x 1-3 x 2+ x 3=6;
в) -3 x 1+5 x 2-2 x 3=5.
Решение. б) В общем виде решения записываются так: (a, b, 6-2 a +3 b), где a и b независимо друг от друга пробегают множество всех чисел. Действительно, 2 a -3 b +(6-2 a +3 b)=6 - верное числовое равенство. Поэтому множество решений данного уравнения записывается так: {(a, b, 6-2 a +3 b) | a, b Î R }.
Ответ: {(a, b, 6-2 a +3 b) | a, b Î R }.
1.1.3. Определение. Пусть даны линейные уравнения:
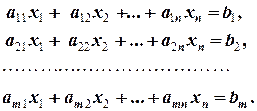 (1.1.2)
(1.1.2)
Если требуется найти общие решения этих уравнений, то говорят, что они образуют систему линейных уравнений. Система, состоящая из уравнений (1.1.2), обозначается следующим образом:
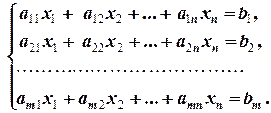 (1.1.3)
(1.1.3)
Общее решение уравнений, составляющих систему, называется решением системы. Если система имеет хотя бы одно решение, то она называется совместной. В противном случае она называется несовместной.
Совместная система, имеющая единственное решение, называется определённой. Если система имеет более одного решения, то она называется неопределённой.
Две системы называются равносильными, если их множества решений совпадают. В частности, несовместные системы равносильны.
Решить систему ¾ это значит либо найти множество всех его решений, либо доказать, что она несовместна.
1.1.4. Определение. Пусть дана система (1.1.3) линейных уравнений. Матрица
A = 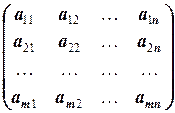
называется (основной) матрицей системы. Матрица
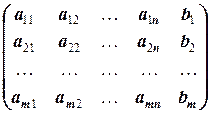
называется расширенной матрицей системы. Столбцы X =(x 1, x 2, …, xn)T и B =(b 1, b 2, …, bm)T называются соответственно столбцами неизвестных и свободных членов.
В расширенной матрице системы столбец свободных членов принято отделять от столбцов коэффициентов вертикальной чертой:
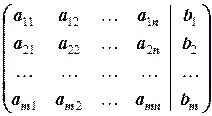
1.1.5. Определение. Элементарными преобразованиями системы называется одно из следующих преобразований:
1) Замена некоторого уравнения системы уравнением, полученным умножением каждого коэффициента при неизвестных и свободного члена этого уравнения на ненулевое число; остальные уравнения остаются без изменения.
2) Замена некоторого уравнения уравнением, полученным прибавлением к коэффициентам и свободному члену данного уравнения соответствующих коэффициентов при неизвестных и свободного члена другого уравнения, умноженных на одно и то же число; остальные уравнения остаются без изменения.
3) Перемена местами двух уравнений системы.
Эти преобразования будем называть преобразованиями соответственно 1- го, 2- го и 3- готипов.
Допуская вольность речи, для краткости преобразование первого типа будем формулировать как умножение некоторого уравнения на ненулевое число, а преобразование второго типа, как прибавление некоторого уравнения, умноженного на число, к другому уравнению.
1.1.6. Теорема. При элементарных преобразованиях системы получается система, равносильная данной.
1.2. Метод Гаусса. Теорема 1.1.6 позволяет к любой системе применить элементарные преобразования для нахождения её решений. При этом некоторые композиции элементарных преобразований позволяют укоротить их последовательное применение. Метод, который основывается на элементарных преобразованиях, называется методом Гаусса.
Метод Гаусса рассмотрим на следующих примерах (в общем случае читателя отсылаем к §2 второй главы первой части данного пособия).
1.2.1. Пример. Решить системы.
a) 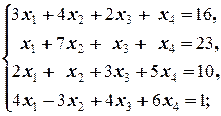 б)
б) 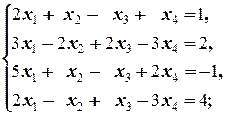
в) 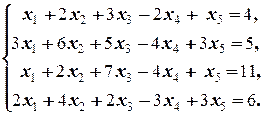
Решение. а) 1) Поменяем местами первое и второе уравнения системы. Тогда получим систему, равносильную данной:
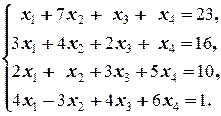
2) Вычтем первое уравнение (полученной системы), умноженное на 3, из второго:
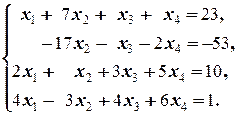
Аналогично, первое уравнение (полученной системы), умноженное на 2, вычитаем из 3-го, и его же, умноженное на 4, вычитаем из 4-го; приходим к системе:
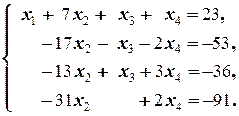
В результате пришли к системе, в которой из уравнений со 2-го по 4-е исключена неизвестная x 1. В этом и заключается метод Гаусса ¾ метод последовательного исключения неизвестных. На следующем шаге из 3-го и 4-го уравнений исключаем неизвестную x 2. Это можно осуществить, например, следующим образом: 2-е уравнение, умноженное на 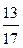 , вычитаем из 3-го, и 2-е уравнение, умноженное на
, вычитаем из 3-го, и 2-е уравнение, умноженное на 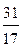 , вычитаем из 4-го. Но в этом случае придётся оперировать дробными коэффициентами, что весьма неудобно. Во избежание этого можно поступить так: из 3-го уравнения, умноженного на 17, вычесть 2-е, умноженное на 13, и из 4-го, умноженного на 17, вычесть 2-е, умноженное на 31. Но и здесь свои неудобства ¾ слишком много арифметических операций, что ведёт к повышению трудоёмкости и вероятности допущения ошибок.
, вычитаем из 4-го. Но в этом случае придётся оперировать дробными коэффициентами, что весьма неудобно. Во избежание этого можно поступить так: из 3-го уравнения, умноженного на 17, вычесть 2-е, умноженное на 13, и из 4-го, умноженного на 17, вычесть 2-е, умноженное на 31. Но и здесь свои неудобства ¾ слишком много арифметических операций, что ведёт к повышению трудоёмкости и вероятности допущения ошибок.
Заметим, что в первом шаге (при исключении неизвестной x 1 из 2-го ¾ 4-го уравнений), мы добились того, что коэффициент при x 1 в 1-м уравнении оказался равным 1. Постараемся, чтобы коэффициент при x 2 во 2-м уравнении равнялся либо 1, либо -1. Для этого
4) сумму 2-го и 3-го уравнений вычтем из 4-го:
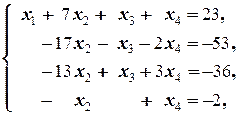
и
5) поменяем местами в полученной системе 2-е и 4-е уравнения:
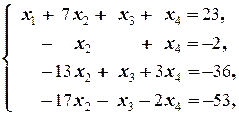
6) В полученной системе 2-е уравнение, умноженное на 13, вычитаем из 3-го, и, умноженное на 17, вычитаем из 4-го:
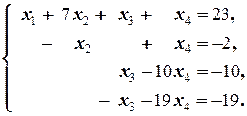
Таким образом, из 3-го и 4-го уравнений исключили неизвестную x 2.
7) Умножим 2-е уравнение на -1, а 3-е прибавим к 4-му:
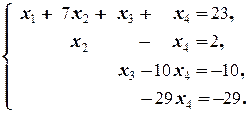
Таким образом, получили систему равносильную исходной, в которой в уравнениях со 2-го по 4-е исключена неизвестная x 1, в 3-м и 4-м исключена неизвестная x 2, в 4-м ¾ неизвестная x 3. Она имеет так называемый «треугольный вид» (под главной диагональю матрицы полученной системы стоят нули, причём диагональные элементы ¾ ненулевые).
8) Из последнего уравнения находим x 4=1, подставляя которое в предпоследнее (3-е), находим x 3=0, а из 2-го находим x 2=3. Наконец, подставляя найденные значения x 2=3, x 3=0 и x 4=1 в 1-е уравнение системы, находим x 1=1.
Ответ: (1; 3; 0; 1).
б) Вычтем из второго уравнения системы первое и поменяем их местами:
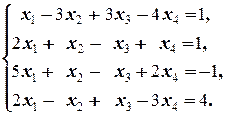
 (1.1.4)
(1.1.4)
Дальше, применяя элементарные преобразования полученной системы, получаем следующую цепочку равносильных систем:
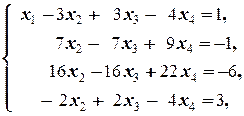
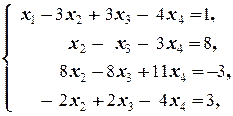
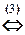
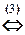
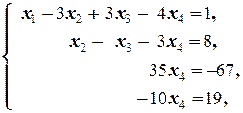
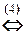
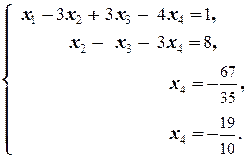
Последние два равенства системы противоречат друг другу, то есть последняя система, и, значит, и исходная, несовместна.
á(1) 1-е уравнение системы (1.1.4), умноженное на 2, вычитаем из 2-го, и, умноженное на 5, вычитаем из 3-го, а 2-е уравнение вычитаем из 4-го.
(2) Последнее уравнение, умноженное на 3, прибавляем ко 2-му, а 3-е делим на 2.
(3) Умножая 2-е уравнение на 8, вычитаем из 3-го, и, умножая его же на 4, прибавляем к 4-му.
(4) Из 3-го и 4-го находим x 4.ñ
Ответ: Система несовместна.
в) Последовательно исключаем переменные:
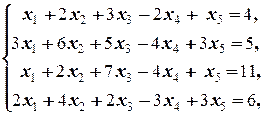
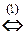
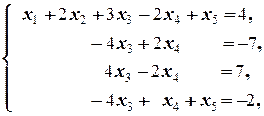
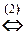
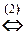
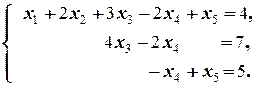
á(1) Исключили из 2-го, 3-го и 4-го уравнений, вычитая 1-е уравнение, умноженное на соответствующие коэффициенты при x 1. При этом оказалось, что из этих уравнений исключена также неизвестная x 2.
(2) 2-е и 3-е уравнения равносильны ¾ они отличаются только знаком. Поэтому одно из них, например, 2-е, исключаем из системы. После этого к последнему уравнению прибавляем 2-е (бывшее 3-е в предыдущей системе).ñ
Таким образом, мы пришли к системе, которая имеет так называемый трапециедальный вид (так мы её называем потому, что её матрица элементарными преобразованиями приводится к трапециедальному виду:
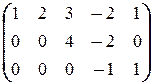 ®
® 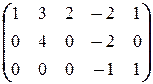 ®
® 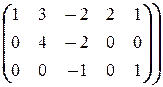
В этой системе, например, x 2 и x 4, могут принимать произвольные значения, скажем, x 2= a, x 4= b. Тогда эта система перепишется в виде
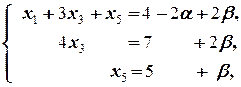
откуда находим последовательно x 3= 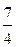 +
+ 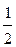 b и x 1= -
b и x 1= - 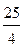 -2 a -
-2 a - 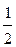 b.
b.
Неизвестные x 2 и x 4 в данном случае ¾ свободные, x 1, x 3, x 5 ¾ связанные. В качестве связанных берутся те неизвестные, коэффициенты при которых в последней системе образуют треугольную матрицу. Поэтому в качестве свободных неизвестных можно было взять x 2 и x 5, а в качестве связанных ¾ x 1, x 3 и x 4.
Рассмотрим решение системы в этом случае, то есть в случае, когда в качестве свободных взяты неизвестные x 2 и x 5, а в качестве связанных ¾ x 1, x 3 и x 4. В этом случае имеем
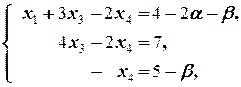
Последовательно находим x 4=-5+ b, x 3= - 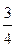 +
+ 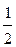 b и x 1= -
b и x 1= - 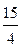 -2 a -
-2 a - 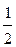 b и множество решений исходной системы запишется так: {(-
b и множество решений исходной системы запишется так: {(- 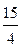 -2 a -
-2 a - 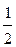 b; a; -
b; a; - 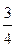 +
+ 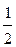 b; -5+ b; b) | a, b Î R }.
b; -5+ b; b) | a, b Î R }.
Ответ: {(- 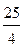 -2 a -
-2 a - 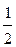 b, a,
b, a, 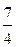 +
+ 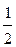 b, b, 5+ b) | a, b Î R } или
b, b, 5+ b) | a, b Î R } или
{(- 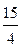 -2 a -
-2 a - 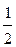 b; a; -
b; a; - 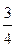 +
+ 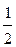 b; -5+ b; b) | a, b Î R }.
b; -5+ b; b) | a, b Î R }.
1.2.2. Упражнения. Решить системы:
а) 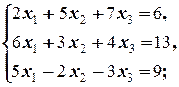 б)
б) 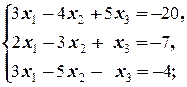
в) 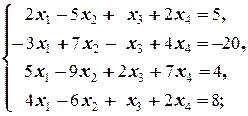 г)
г) 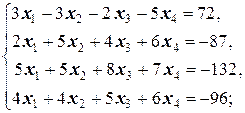
1.2.3. Упражнения. Решить системы:
а) 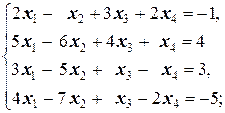 б)
б) 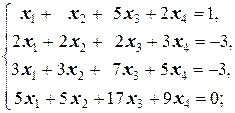
в) 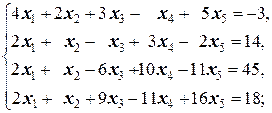 д)
д) 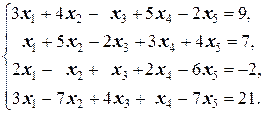
1.2.4. Упражнения. Решить системы:
а) 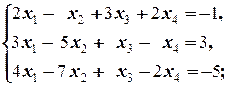 б)
б) 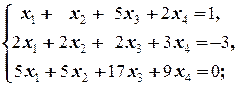
в) 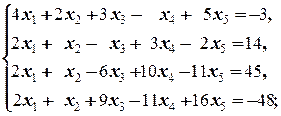 д)
д) 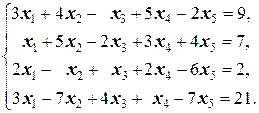
1.2.5. Замечание. Решение системы методом Гаусса можно свести к элементарным преобразованиям строк её расширенной матрицы. Действительно, работая с системой, мы работаем, по существу, с коэффициентами и свободными членами уравнений системы, из которых составлена её матрица. Продемонстрируем это на примере 1.2.1.
а) Выпишем расширенную матрицу системы и применим к ней преобразования, соответствующие преобразованиям 1) ¾ 7) исходной системы. В результате получим следующую цепочку преобразований матрицы:
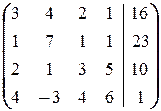 ®
® 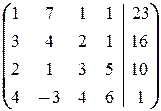 ®
® 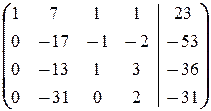 ®
®
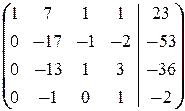 ®
® 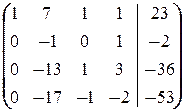 ®
® 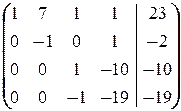 ®
®
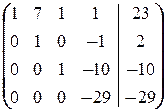
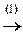 Ä
Ä
Продолжая преобразовывать строки последней матрицы так, чтобы основная матрица обратилась в единичную, получаем продолжение этой цепочки:
Ä 
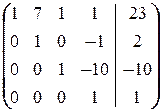
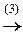
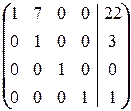
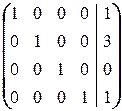 . Это значит, что
. Это значит, что 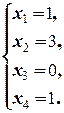
á(1) Разделили последнюю строку на -29.
(2) Последнюю строку вычли из 1-й, прибавили ко 2-й, и, умноженную на 10, прибавили к 3-й.
(3) 3-ю строку вычли из 1-й.
(4) 2-ю строку, умноженную на 7, вычли из 1-й.ñ
Аналогично имеем
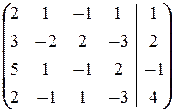 ®
® 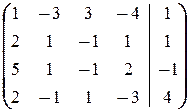 ®
® 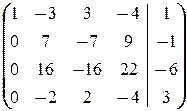 ®
® 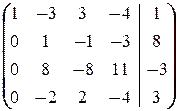 ®
® 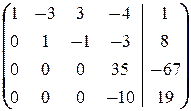 ®
® 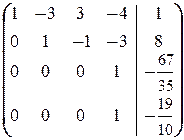 .
.
Последние две строки означают, что x 4= - 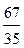 и x 4= -
и x 4= - 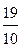 ¾ противоречие.
¾ противоречие.
в) 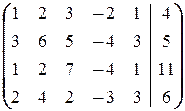 ®
® 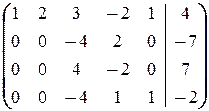
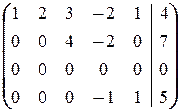
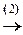
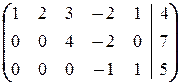 ® Ä
® Ä
á(1) Поменяли 2-ю и 3-ю строки и к 3-ей строке прибавили 2-ю.
(2) Из рассмотрения исключается 3-я строка, соответствующая равенству 0=0.ñ
Далее, перенесём вправо от вертикальной черты 2-й и 4-й столбцы, поменяв знаки при элементах на противоположные. Это соответствует тому, что неизвестным x 2 и x 4 придаются свободные значения a и b соответственно, и они переносятся в правую часть. В левой части остаются связанные неизвестные, коэффициенты при которых образуют треугольную подматрицу, после чего эта подматрица элементарными преобразованиями строк преобразуется в единичную:
Ä ® 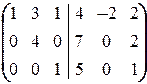
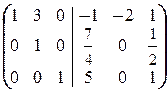
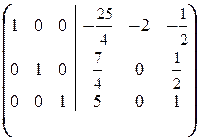
Последняя матрица означает, что 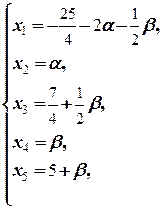 где a, b Î R.
где a, b Î R.
á(3) Из 1-й строки вычли последнюю.
(4) 2-ю строку, умноженную на 3, вычли из 1-й.ñ
1.2.6. Упражнения. Решить системы, применив элементарные преобразования расширенной матрицы системы:
а) 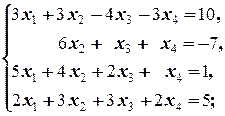 б)
б) 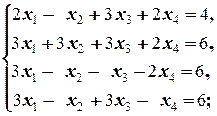
в) 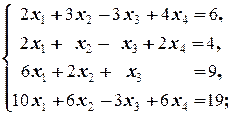 г)
г) 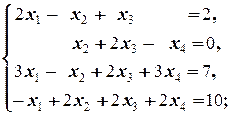
д) 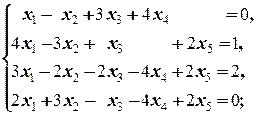 е)
е) 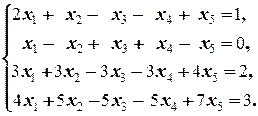
1.3. Метод Жордана-Гаусса. Этот метод - модифицированный вариант метода Гаусса. Он заключается в том, что очередная неизвестная исключается из всех уравнений, кроме одного уравнения, а в уравнении, из которого она не исключается, коэффициент при неизвестной приводится к 1. В результате, если система совместна, она приводится к виду
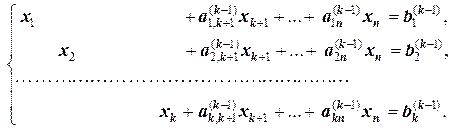 (1.3.1).
(1.3.1).
Полученная система (1.3.1) позволяет сразу выписать общее решение исходной системы. Кроме того, данный метод применим в некоторых приложениях теории систем линейных уравнений, например, в так называемом симплекс - методе при решении основной задачи линейного программирования.
1.4. В заключение параграфа введём некоторые дальнейшие понятия и сделаем ряд замечаний, относящихся к методам Гаусса и Жордана-Гаусса.
Как известно, ранг матрицы (П3, 3.3.2) определяется по ненулевому минору (П3, 3.3.2) максимального порядка.
1.4.1. Определение. Базисным минором системы называется ненулевой минор максимального порядка матрицы системы. Неизвестные системы, коэффициенты которых образуют некоторый базисный минор, называются базисными.
Так как базисных миноров, вообще говоря, не один, то и групп базисных неизвестных - не одна.
Если зафиксированы базисные неизвестные, то остальные неизвестные называются свободными.
Так, в системе (1.3.1) неизвестные х 1, х 2, …, хk - базисные, а остальные - свободные.
В методах Гаусса и Жордана-Гаусса исключаются как раз базисные неизвестные. Исключение неизвестных можно начинать с любой, например, с той, у которой коэффициент равен ±1. На очередном шаге выбирается та неизвестная, коэффициент при которой не равен нулю. Например, после исключения х 1 коэффициент при х 2 может оказаться равным нулю и тогда можно выбирать любую неизвестную хl, для которой в системе (1.2.3) 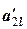 ¹0. Как правило, выбирают такую хl, что
¹0. Как правило, выбирают такую хl, что 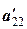 =…=
=…= 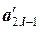 =0, а
=0, а 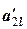 ¹0. И т.д. Либо выбирают такую хl, что
¹0. И т.д. Либо выбирают такую хl, что 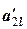 = ±1. Поэтому, вообще говоря, матрица окончательной системы имеет вид, в котором под ненулевыми элементами некоторой строки (некоторых строк) стоят сразу несколько нулей:
= ±1. Поэтому, вообще говоря, матрица окончательной системы имеет вид, в котором под ненулевыми элементами некоторой строки (некоторых строк) стоят сразу несколько нулей:
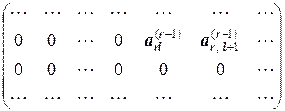
где 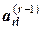 ¹0 и
¹0 и 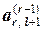 ¹0.
¹0.
1.4.2. Определение. Ведущей неизвестной шага называется неизвестная, которая исключается на данном шаге. То уравнение, с помощью которого она исключается, и в котором она остаётся, называется ведущим уравнением. В методе Жордана-Гаусса это то уравнение, в котором ведущая неизвестная остаётся.
1.4.3. Преобразование системы, равносильно элементарным преобразованиям строк её расширенной матрицы. В этом случае вместо термина «ведущая неизвестная» применяется понятие ведущий столбец, а вместо термина «ведущее уравнение» - ведущая строка.
1.4.4. Определение. Уравнение
(b 1 а 11+ b 2 а 21+…+ bkаk 1) х 1+(b 1 а 12+ b 2 а 22+…+ bkаk 2) х 2+…+(b 1 а 1 n + b 2 а 2 n +…+ bkаkn) хn =
= b 1 b 1+ b 2 b 2+…+ bkbk (1.4.1)
называется линейной комбинацией уравнений
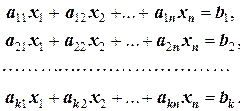 (1.4.2)
(1.4.2)
1.4.5. Определение. Уравнения (1.4.2) называются линейно независимыми, если из равенства нулю всех коэффициентов при неизвестных и свободного члена в линейной комбинации (1.4.1) следует, что b 1= b 2=…= bk =0. В противном случае эти уравнения называются линейно зависимыми. Другими словами, уравнения (1.4.2) линейно зависимы, если существуют не все равные нулю b 1, b 2, …, bk такие, что в линейной комбинации (1.4.1) все коэффициенты при неизвестных и свободный член равны нулю.
1.4.6. Линейная комбинация некоторых уравнений системы равносильна линейной комбинации соответствующих строк расширенной матрицы системы; аналогично, линейная зависимость (независимость) уравнений системы равносильна линейной зависимости (независимости) соответствующих строк расширенной матрицы системы.
1.4.7. Предложение. Если из системы исключить уравнения, являющиеся линейными комбинациями одних и тех же линейно независимых уравнений системы, то получится система, равносильная исходной.
 2015-03-08
2015-03-08 2265
2265
