2.2.1. Определение. Пусть даны линейные уравнения
a 1 x + b 1 y + c 1 z = d 1,(2.2.1)
a 2 x + b 2 y + c 2 z = d 2. (2.2.2)
Если требуется найти общее решение уравнений (2.2.1) и (2.2.2), то говорят, что они образуют систему. Система, состоящая из уравнений (2.2.1) и (2.2.2), обозначается следующим образом:
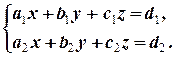 (2.2.3)
(2.2.3)
Общее решение уравнений, составляющих систему, называется решением системы. Решить систему (2.2.3) ¾ это значит либо найти множество всех его решений, либо доказать, что их нет.
Ниже мы сформулируем условия, при которых система (2.2.3) имеет более одного решения и не имеет ни одного решения (теорема 2.2.4).
2.2.2. Определение. Пусть дана система (2.2.3) линейных уравнений. Матрица 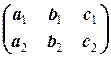 называется (основной) матрицей системы. Матрица
называется (основной) матрицей системы. Матрица 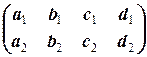 называется расширенной матрицей системы.
называется расширенной матрицей системы.
Определения равносильных систем, элементарных преобразований систем вводятся аналогично, как и для систем из двух уравнений с двумя неизвестными. Кроме того, напоминаем, что при элементарных преобразованиях системы получается система, равносильная данной.
Это обстоятельство позволяет легко решить систему (2.2.3) с помощью элементарных преобразований.
2.2.3. Пример. Решить системы уравнений:
а) 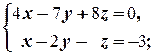 б)
б) 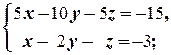 в)
в) 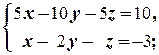
г) 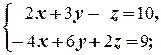 д)
д) 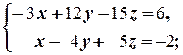 е)
е) 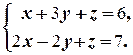
Решение. а)
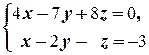
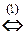
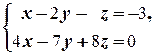
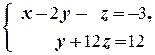
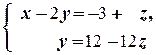
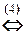
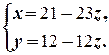
Неизвестная z может принимать любое числовое значение a. Тогда x =21-23 a и y =12-12 a. Таким образом, множество решений системы: {(21-23 a; 12-12 a; a)| a Î R }.
á(1) Поменяли местами уравнения (преобразование 3-го типа).
(2) Первое уравнение, умноженное на 4, вычли из второго (преобразование 2-го типа).
(3) Перенесли из левых уравнений в правую члены с неизвестной z (поменяв знаки на противоположные)
(4) В первое уравнение вместо y подставили его выражение через z: y =12-12 z. ñ
Замечание. Вместо z в правые части мы могли перенести y, и тогда множество решений записалось бы в виде {(-2+ 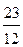 b; b; 1-
b; b; 1- 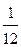 b)| b Î R }. Естественно, множества {(21-23 a; 12-12 a; a)| a Î R } и {(-2+
b)| b Î R }. Естественно, множества {(21-23 a; 12-12 a; a)| a Î R } и {(-2+ 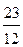 b; b; 1-
b; b; 1- 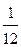 b)| b Î R } совпадают.
b)| b Î R } совпадают.
б) Разделим первое уравнение на 5. Тогда приходим к системе 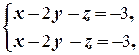 которая равносильна уравнению x -2 y - z = -3. Она равносильна уравнению x = -3+2 y + z, где неизвестные y и z могут принимать любые значения y = a и z = b. Таким образом, множество всех решений системы ¾ следующее: {(-3+2 a + b; a; b)| a, b Î R }.
которая равносильна уравнению x -2 y - z = -3. Она равносильна уравнению x = -3+2 y + z, где неизвестные y и z могут принимать любые значения y = a и z = b. Таким образом, множество всех решений системы ¾ следующее: {(-3+2 a + b; a; b)| a, b Î R }.
в) Разделим первое уравнение на 5 и вычтем из последнего. Придём к равносильной системе 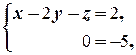 второе уравнение которой является противоречивым. Следовательно, система решений не имеет.
второе уравнение которой является противоречивым. Следовательно, система решений не имеет.
Ответ: а) (21-23 a; 12-12 a; a), a Î R;
б) {(-3+2 a + b; a; b)| a, b Î R };
в) Система решений не имеет.
Из предыдущих примеров видно, что система из двух уравнений с тремя неизвестными может иметь бесконечное множество решений, а может вообще их не иметь.
2.2.4. Теорема. Пусть дана система (3.2.3), d 1= 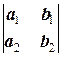 , d 2=
, d 2= 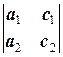 , d 3=
, d 3= 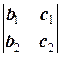 , D1=
, D1= 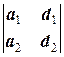 , D2=
, D2= 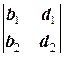 и D3=
и D3= 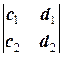 . Тогда:
. Тогда:
1) Если хотя бы один из определителей d 1, d 2 или d 3 не равен нулю, то система имеет бесконечное множество решений, зависящих от одного параметра.
2) Если d 1= d 2= d 3=0 и хотя бы один из определителей D1, D2 или D3 не равен нулю, то система решений не имеет.
3) Если d 1= d 2= d 3=D1=D2=D3=0, то система имеет бесконечное множество решений, зависящих от двух параметров.
Замечание. Условие D1=0 равносильно D2=0 или D3=0; так что некоторые из этих условий в формулировке теоремы 3.2.4 излишние.
2.2.5. Упражнение. Решить системы, предварительно исследовав их на наличие решений:
а) 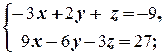 б)
б) 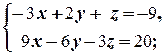 в)
в) 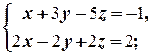
г) 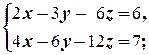 д)
д) 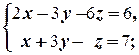 е)
е) 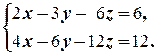
Решение. а) Так как d 1= 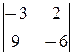 =0, d 2=
=0, d 2= 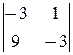 =0, d 3=
=0, d 3= 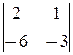 =0, D1=
=0, D1= 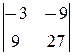 =0, D2=
=0, D2= 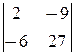 =0, D3=
=0, D3= 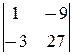 =0, то система имеет бесконечное множество решений, зависящих от двух параметров. Найдем их. Эта система равносильна уравнению -3 x +2 y + z = -9 (второе уравнение получается из этого умножением на -3). Положив y = a и z = b, получаем x =3+
=0, то система имеет бесконечное множество решений, зависящих от двух параметров. Найдем их. Эта система равносильна уравнению -3 x +2 y + z = -9 (второе уравнение получается из этого умножением на -3). Положив y = a и z = b, получаем x =3+ 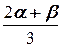 . Тогда (3+
. Тогда (3+ 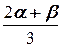 , a, b) ¾ решение системы, a, b Î R.
, a, b) ¾ решение системы, a, b Î R.
б) С одной стороны, d 1= 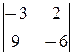 =0, d 2=
=0, d 2= 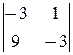 =0, d 3=
=0, d 3= 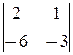 =0, с другой, D1=
=0, с другой, D1= 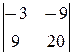 =21¹0. Поэтому система решений не имеет.
=21¹0. Поэтому система решений не имеет.
в) Так как d 1= 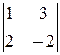 =-8¹0, то система имеет бесконечное множество решений, зависящих от одного параметра. Найдём их:
=-8¹0, то система имеет бесконечное множество решений, зависящих от одного параметра. Найдём их:
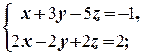
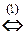
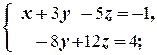
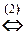
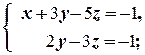
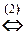
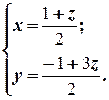
Полагая z = a, получаем множество всех решений системы: {(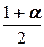 ,
, 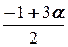 , a) | a Î R }.
, a) | a Î R }.
 2015-03-08
2015-03-08 10197
10197
