2.3.1. Определение.
Пусть даны линейные уравнения:
a 1 x + b 1 y + c 1 z = d 1, (2.3.1)
a 2 x + b 2 y + c 2 z = d 2, (2.3.2)
a 3 x + b 3 y + c 3 z = d 3. (2.3.3)
Если требуется найти общее решение уравнений (2.3.1) ¾ (2.3.3), то говорят, что они образуют систему. Система, состоящая из уравнений (2.3.1) ¾ (2.3.3), обозначается следующим образом:
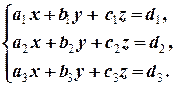 (2.3.4)
(2.3.4)
Общее решение уравнений, составляющих систему, называется решением системы. Решить систему (2.3.4) ¾ это значит либо найти множество всех его решений, либо доказать, что их нет.
Как и в предыдущих случаях, ниже мы найдем условия, при которых система (2.3.4) имеет единственное решение, имеет более одного решения и не имеет ни одного решения.
2.3.2. Определение. Пусть дана система (2.3.4) линейных уравнений. Матрицы
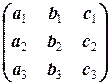 и
и 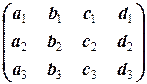
называются соответственно (основной) матрицей и расширенной матрицей системы.
2.3.3. Определения равносильных систем вида (2.3.4), а также элементарных преобразований 1-го и 2-го типов вводятся аналогично, как и для систем из двух уравнений с двумя и тремя неизвестными.
Элементарным преобразованием 3-го типа системы (2.3.4) называется перемена местами некоторых двух уравнений этой системы. Аналогично предыдущим случаям систем из 2-х уравнений при элементарных преобразованиях системы получается система, равносильная данной.
2.3.4. Упражнение. Решить системы уравнений:
а) 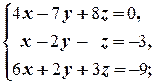 б)
б) 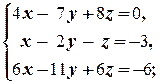 в)
в) 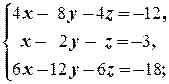
г) 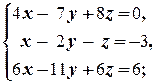 д)
д) 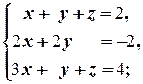 е)
е) 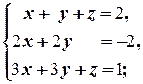
ж) 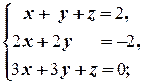 з)
з) 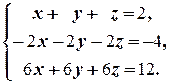
Решение. а)
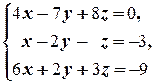
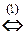
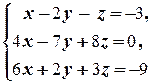
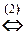
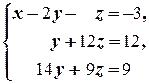
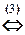
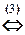
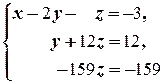
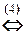
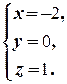
(1) Поменяли местами первое и второе уравнения системы (преобразование 3-го типа).
(2) Первое уравнение, умноженное на 4, вычли из второго, и первое уравнение, умноженное на 6, вычли из третьего (преобразование 2-го типа); таким образом, из второго и третьего уравнений исключили неизвестную x.
(3) Второе уравнение, умноженное на 14, вычли из третьего; из третьего исключили неизвестную y.
(4) Из последнего уравнения находим z = 1, подставляя которое во второе, находим y = 0. Наконец, подставляя y = 0 и z = 1 в первое уравнение, находим x = -2.ñ
б) 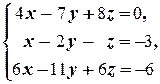
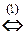
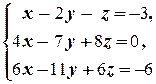
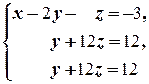
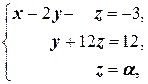
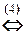
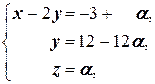
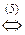
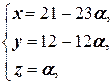
(1) Поменяли местами первое и второе уравнения системы.
(2) Первое уравнение, умноженное на 4, вычли из второго, и первое уравнение, умноженное на 6, вычли из третьего.
(3) Второе и третье уравнения совпали. Одно из них исключаем из системы (или, по-другому, если вычесть из третьего уравнения второе, то третье уравнение обратится в тождество 0 = 0;оно исключается из системы. Полагаем z = a.
(4) Подставляем z = a во второе и первое уравнения.
(5) Подставляя y = 12 - 12 a в первое уравнение, находим x.
в) Если первое уравнение разделить на 4, а третье ¾ на 6, то придём к равносильной системе
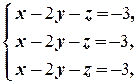
которая равносильна уравнению x - 2 y - z = -3. Решения этого уравнения известны (см. Пример 2.2.3 б))
г) 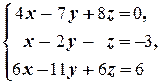
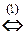
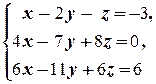
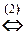
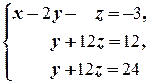
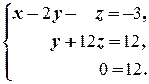
Последнее равенство в полученной системе является противоречивым. Следовательно, система решений не имеет.
Преобразования (1) и (2) ¾ точно такие же, как и соответствующие преобразования системы б))
(3) Из последнего уравнения вычли второе.
Ответ: а) (-2; 0; 1);
б) (21 - 23 a; 12 - 12 a; a), a Î R;
в) {(-3 + 2 a + b; a; b)| a, b Î R };
г) Система решений не имеет.
2.3.5. Из предыдущих примеров вытекает, что система с тремя неизвестными, как и система с двумя неизвестными, может иметь единственное решение, бесконечное множество решений и не иметь ни одного решения. Ниже мы разберём все возможные случаи. Но предварительно введём некоторые обозначения.
Через D обозначим определитель матрицы системы:
D= 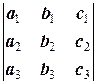 .
.
Через D1 обозначим определитель, полученный из D заменой первого столбца на столбец свободных членов:
D1= 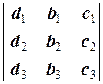 .
.
Аналогично, положим
D2= 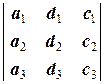 и D3=
и D3= 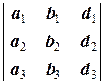 .
.
2.3.6. Теорема. Если D¹0, то система (2.3.4) имеет единственное решение
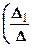 ,
, 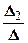 ,
, 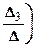 . (2.3.5)
. (2.3.5)
Формулы (2.3.5) называются формулами Крамера.
3.3.7. Упражнение. Решить системы по формулам Крамера.
а) 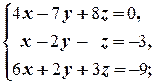 б)
б) 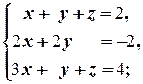 в)
в) 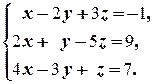
Следующая теорема ¾ о множестве решений системы (2.3.4) для случая, когда D=0.
2.3.8. Теорема. Пусть дана система (2.3.4), D ¾ определитель системы и D=0. Тогда:
1) Если хотя бы один из определителей D1, D2 или D3 не равен нулю, то система решений не имеет.
2) Если хотя бы один из определителей 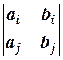 ,
, 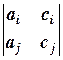 или
или 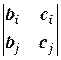 (i ¹ j) не равен нулю и D1 = D2 = D3 = 0, то система имеет бесконечное множество решений, зависящих от одного параметра.
(i ¹ j) не равен нулю и D1 = D2 = D3 = 0, то система имеет бесконечное множество решений, зависящих от одного параметра.
3) Если 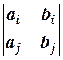 =
= 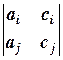 =
= 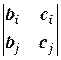 = 0 для всех i ¹ j и хотя бы один из определителей
= 0 для всех i ¹ j и хотя бы один из определителей 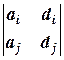 ,
, 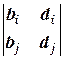 ,
, 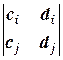 не равен нулю, то система решений не имеет.
не равен нулю, то система решений не имеет.
4) Если 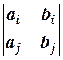 =
= 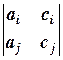 =
= 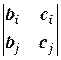 =
= 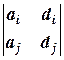 =
= 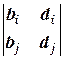 =
= 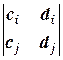 = 0 для всех i ¹ j, то система имеет бесконечное множество решений, зависящих от двух параметров.
= 0 для всех i ¹ j, то система имеет бесконечное множество решений, зависящих от двух параметров.
2.3.9. Упражнение. Исследовать системы упражнения 2.3.4 на наличие решений и решить их.
 2015-03-08
2015-03-08 31890
31890
