Частные методы решения систем

В этом параграфе мы рассмотрим методы решения систем линейных уравнений, отличных от метода Гаусса. Их можно, действительно, назвать частными, так как одни из них предназначены для решения определённых систем, другие ¾ для решения неопределённых систем. Кроме того, приведём критерий совместности системы, применение которого также в определённой степени можно назвать частным методом, так как в случае несовместности системы применение этого критерия даёт ответ.

Но прежде введём некоторые понятия.

Множество всех решений системы назовём общим решением. Отдельно взятое решение неопределённой системы назовём её частным решением.

2.1. Матричный метод и правило Крамера. Матричный метод и правило Крамера решения систем применяются к системам, в которых число уравнений совпадает с числом неизвестных:

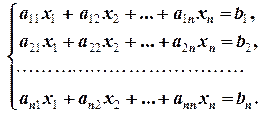(2.1.1)

2.1.1. Теорема. Если определитель системы (2.1.1) не равен нулю, то она имеет единственное решение, которое можно найти по формуле

X = A 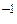B, (2.1.2)

где A ¾ матрица системы, X и B ¾ столбцы соответственно неизвестных и свободных членов.

Формула (2.1.2) даёт так называемый матричный метод решения системы.

2.1.2. Пример. Решить систему матричным методом:

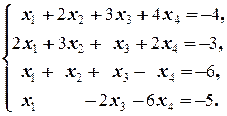
Решение. Найдём определитель системы:

D= 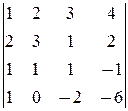= -1¹0.

Определитель системы ненулевой. Следовательно, матричный метод применим. Найдём A 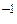. Имеем

A =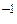

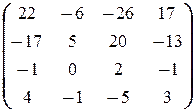
(правило нахождения обратной матрицы см. Приложение 3.3). Поэтому по формуле (2.1.2) имеем

X = = = = ,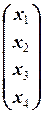

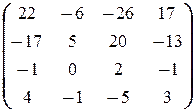
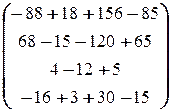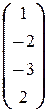то есть = .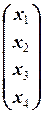

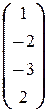Ответ: (1; -2; -3; 2).

Обозначим через D определитель матрицы системы:

D= .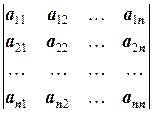

Через D₁ обозначим определитель, полученный из D заменой первого столбца на столбец свободных членов:

D₁= .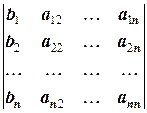

Аналогично, положим

D₂= 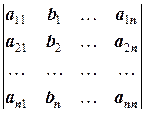и, вообще, D _i = 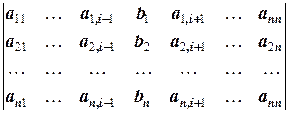¾ определитель, полученный из определителя D заменой i -го столбца на столбец свободных членов системы.

2.1.3. Теорема. Если D¹0, то система (2.1.1) имеет единственное решение , , …, .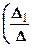

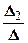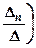2.1.4. Пример. Решить систему из примера 2.1.2, пользуясь правилом Крамера.

Решение. Так как D= -1¹0, то к системе применимо правило Крамера. Найдём D _i для всех i =1, 2, 3, 4. D₁ ¾ определитель, полученный из D заменой 1-го столбца на столбец свободных членов, D₂ ¾ определитель, полученный из D заменой 2-го столбца на столбец свободных членов и т.д. Поэтому

D₁= 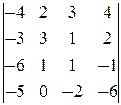= -1; D₂= 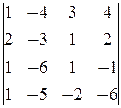=2; D₃= 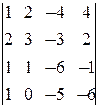=3; D₄= 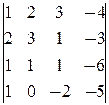= -2.

Тогда x ₁= 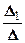= =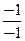1; x ₂= 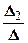= = 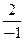-2; x ₃= 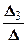= = 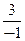-3; x ₄= 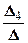= =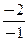2.

Ответ: (1; -2; -3; 2).

2.2.5. Упражнение. Решить системы из Упражнения 1.2.2 правилом Крамера и матричным методом.