3.2.1. Определение. Матрица B называется обратной к матрицеA, если она удовлетворяет условию AB = BA = E.
Матрица, обратная к A, обозначается через A 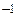 .
.
3.2.2. Теорема. Обратная к матрице A существует тогда и только тогда, когда A является квадратной и det A ¹0. При этом
A 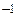 = (det A)
= (det A) 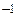 ×
× 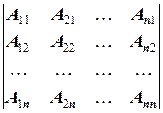 , (3.1)
, (3.1)
где n - размерность A, Aij - алгебраическое дополнение элемента aij матрицы A.
Таким образом, для того, чтобы найти обратную матрицу, прежде всего, необходимо убедиться, что det A ¹0. И если det A =0, то обратная не существует и искать нечего. Если det A ¹0, то можно применить формулу (3.1).
Например, найдём обратную к А = 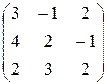 . Прежде всего, убеждаемся, что det A ¹0:
. Прежде всего, убеждаемся, что det A ¹0:
det A = 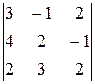 =3×2×2+4×3×2+2×(-1)×(-1)-2×2×2-4×(-1)×2-3×3×(-1)=47.
=3×2×2+4×3×2+2×(-1)×(-1)-2×2×2-4×(-1)×2-3×3×(-1)=47.
Таким образом, det A ¹0. Значит, A  существует.
существует.
В нашем случае
A  =
= 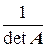
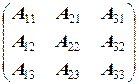 .
.
Имеем
A 11=(-1)1+1 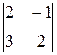 =2×2-3×(-1)=7; A 21=(-1)2+1
=2×2-3×(-1)=7; A 21=(-1)2+1 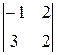 =-((-1)×2-3×2)=8;
=-((-1)×2-3×2)=8;
A 31=(-1)3+1 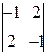 =(-1)×(-1)-2×2=-3; A 12=(-1)1+2
=(-1)×(-1)-2×2=-3; A 12=(-1)1+2 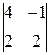 =-(4×2-2×(-1))=-10;
=-(4×2-2×(-1))=-10;
A 22=(-1)2+2 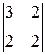 =3×2-2×2=2; A 32=(-1)3+2
=3×2-2×2=2; A 32=(-1)3+2 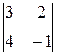 =-(3×(-1)-4×2)=11;
=-(3×(-1)-4×2)=11;
A 13=(-1)1+3 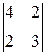 =4×3-2×2=8; A 23=(-1)2+3
=4×3-2×2=8; A 23=(-1)2+3 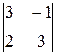 =-(3×3-2×(-1))=-11;
=-(3×3-2×(-1))=-11;
A 33=(-1)3+3 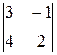 =3×2-4×(-1)=10.
=3×2-4×(-1)=10.
Поэтому
A 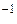 =
= 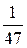
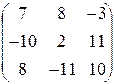 =
= 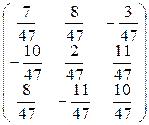 , то есть A
, то есть A 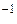 =
= 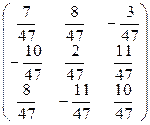 .
.
Проверка:
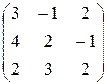 ×
× 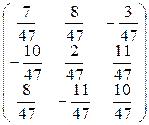 =
=
= 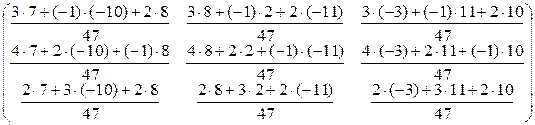 =
=
= 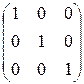 ,
,
То есть 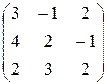 ×
× 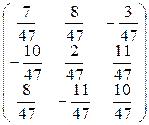 =
=  .
.
Замечание. После нахождения обратной матрицы проверка желательна (хотя и необязательна), так как в силу большого количества арифметических операций вероятность их ошибок возрастает.
3.2.3. Другой метод нахождения обратной матрицы основывается на элементарных преобразованиях строк и заключается в следующем:
1) К матрице А (обратную к которой требуется найти) приписывается единичная той же размерности, что и А: А | E.
2) К матрице А | E (размерности n ´2 n) применяем элементарные преобразования строк так, чтобы привести её к виду E | B. Тогда B = A  .
.
Ясно, что если A 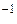 не существует, то на каком-то шаге мы придём к матрице А 1| E 1 такой, что некоторые строки А 1 будут нулевыми, и дальнейшие преобразования с целью приведения к виду E | B становятся невозможными.
не существует, то на каком-то шаге мы придём к матрице А 1| E 1 такой, что некоторые строки А 1 будут нулевыми, и дальнейшие преобразования с целью приведения к виду E | B становятся невозможными.
Найдём элементарными преобразованиями, например, матрицу, обратную к А предыдущего примера.
Припишем к А единичную и подвергнем элементарным преобразованиям строк полученную матрицу:
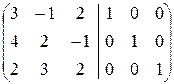
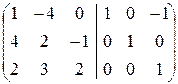
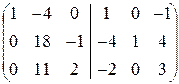
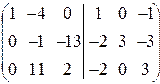
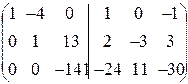
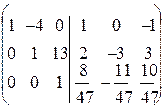
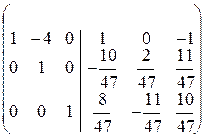
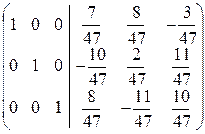
á(1) Из первой строки вычли третью.
(2) Первую строку, умноженную на 4 и 2, вычли из второй и третьей соответственно.
(3) Из второй строки, умноженной на 3, вычли третью, умноженную на 5.
(4) Вторую строку, умноженную на 11, прибавили к третьей; вторую строку переписали с противоположным знаком (умножили на -1).
(5) Третью строку разделили на -141.
(6) Третью строку, умноженную на 13, вычли из второй.
(7) К первой строке прибавили вторую, умноженную на 4.ñ
На месте единичной матрицы Е получилась матрица
B = A 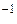 =
= 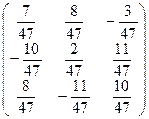 .
.
Как видим, она совпала с матрицей, вычисленной по формуле (3.1).
 2015-03-08
2015-03-08 804
804








