3.3.1. Найти ранг матрицы методом окаймления миноров и с помощью элементарных преобразований:
а) 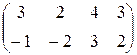 ; б)
; б) 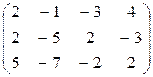 ;
;
в) 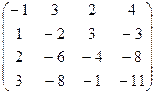 ; г)
; г) 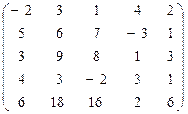 .
.
3.3.2. Найти матрицу, обратную данной, двумя способами:
а) 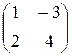 ; б)
; б) 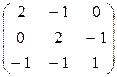 ;
;
в) 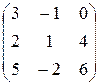 ; г)
; г) 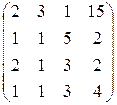 .
.
Приложения
Приложение 1. Варианты индивидуальных заданий
Варианты индивидуальных заданий приведены ниже в таблице. Во всех вариантах предлагается выполнить следующие задания:
Задание 1. Вычислить выражение А 2+2 АВ -5 В Т А Т.
Задание 2. Найти определитель матрицы.
Задание 3. Найти ранг матрицы двумя методами:
а) методом окаймления миноров;
б) с помощью элементарных преобразований.
Задание 4. Найти матрицу, обратную данной двумя методами.
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 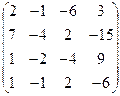 , В = , В = 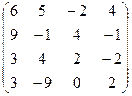 | А = 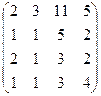 , В = , В = 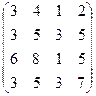 | А = 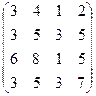 , В = , В = 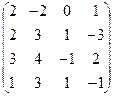 | А = 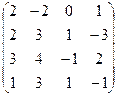 , В = , В = 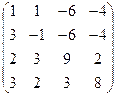 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
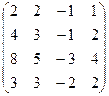 | 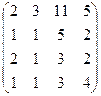 | 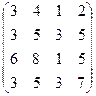 | 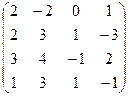 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
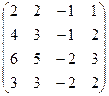 | 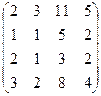 | 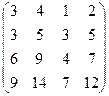 | 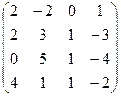 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 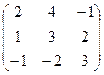 б) б) 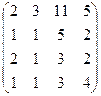 | а) 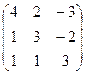 б) б) 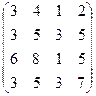 | а) 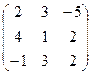 б) б) 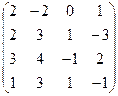 | а) 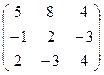 б) б) 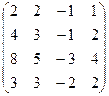 |
| Вариант 5 | Вариант 6 | Вариант 7 | Вариант 8 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 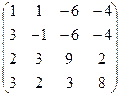 , В = , В = 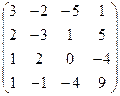 | А = 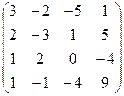 , В = , В = 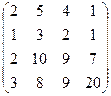 | А = 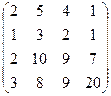 , В = , В = 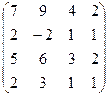 | А = 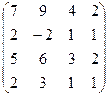 , В = , В = 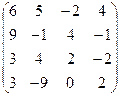 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
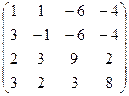 | 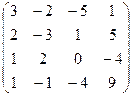 | 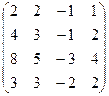 | 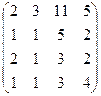 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
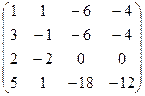 | 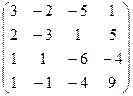 | 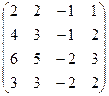 | 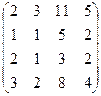 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 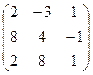 б) б) 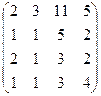 | а) 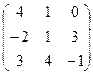 б) б) 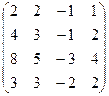 | а) 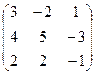 б) б) 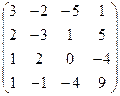 | а) 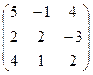 б) б) 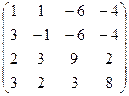 |
| Вариант 9 | Вариант 10 | Вариант 11 | Вариант 12 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 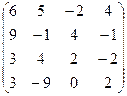 , В = , В = 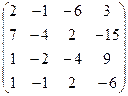 | А = 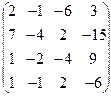 , В = , В = 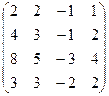 | А = 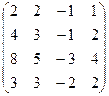 , В = , В = 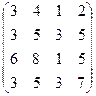 | А = 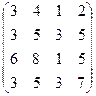 , В = , В = 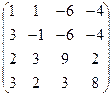 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
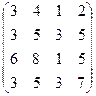 | 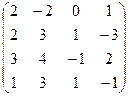 | 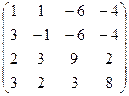 | 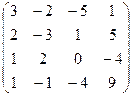 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
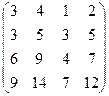 | 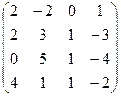 | 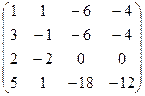 | 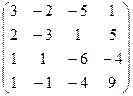 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 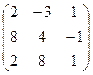 б) б) 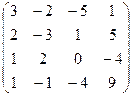 | а) 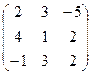 б) б) 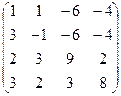 | а) 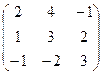 б) б) 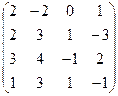 | а) 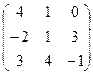 б) б) 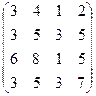 |
| Вариант 13 | Вариант 14 | Вариант 15 | Вариант 16 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 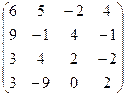 , В = , В = 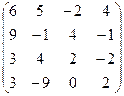 | А = 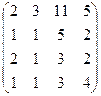 , В = , В = 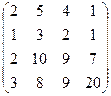 | А = 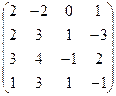 , В = , В = 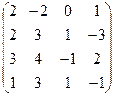 | А = 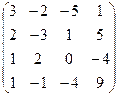 , В = , В = 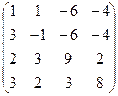 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
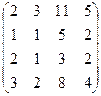 | 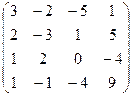 | 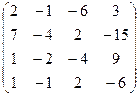 | 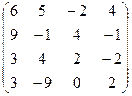 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
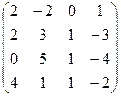 | 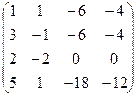 | 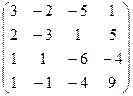 | 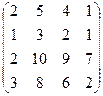 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 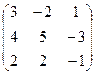 б) б) 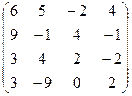 | а) 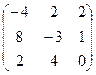 б) б) 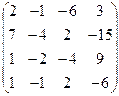 | а) 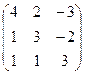 б) б) 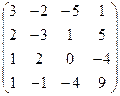 | а) 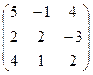 б) б) 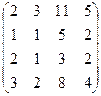 |
| Вариант 17 | Вариант 18 | Вариант 19 | Вариант 20 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 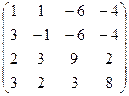 , В = , В = 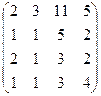 | А = 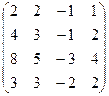 , В = , В = 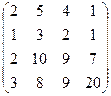 | А = 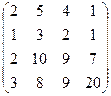 , В = , В = 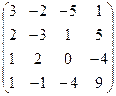 | А = 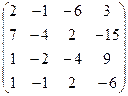 , В = , В = 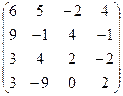 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
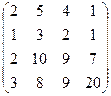 | 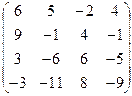 | 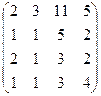 | 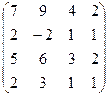 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
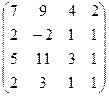 | 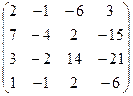 | 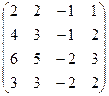 | 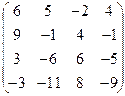 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 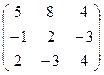 б) б) 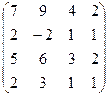 | а) 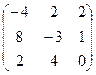 б) б) 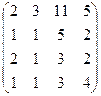 | а) 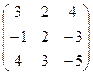 б) б) 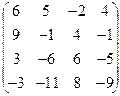 | а) 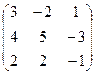 б) б) 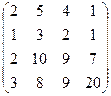 |
| Вариант 21 | Вариант 22 | Вариант 23 | Вариант 24 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 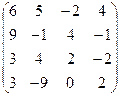 , В = , В = 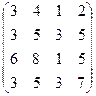 | А = 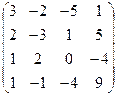 , В = , В = 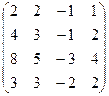 | А = 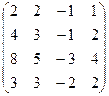 , В = , В = 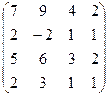 | А = 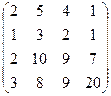 , В = , В = 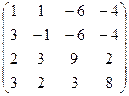 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
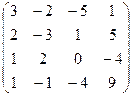 | 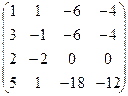 | 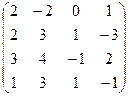 | 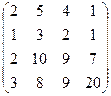 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
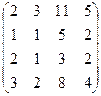 | 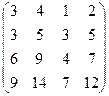 | 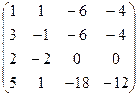 | 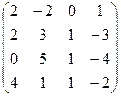 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 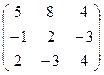 б) б) 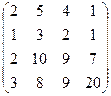 | а) 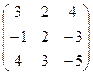 б) б) 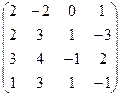 | а) 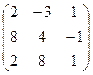 б) б) 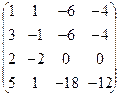 | а) 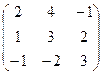 б) б) 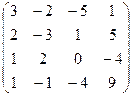 |
| Вариант 25 | Вариант 26 | Вариант 27 | Вариант 28 |
| Задание 1 | Задание 1 | Задание 1 | Задание 1 |
А = 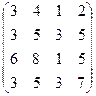 , В = , В = 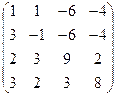 | А = 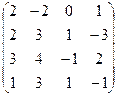 , В = , В = 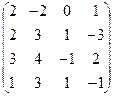 | А = 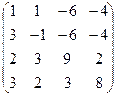 , В = , В = 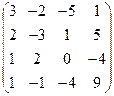 | А = 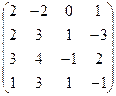 , В = , В = 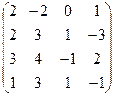 |
| Задание 2 | Задание 2 | Задание 2 | Задание 2 |
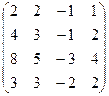 | 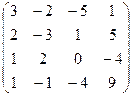 | 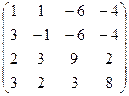 | 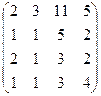 |
| Задание 3 | Задание 3 | Задание 3 | Задание 3 |
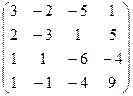 | 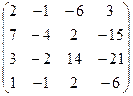 | 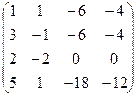 | 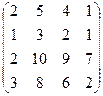 |
| Задание 4 | Задание 4 | Задание 4 | Задание 4 |
а) 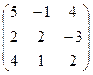 б) б) 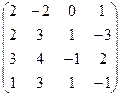 | а) 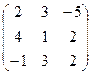 б) б) 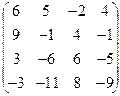 | а) 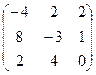 б) б) 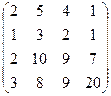 | а) 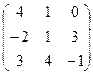 б) б) 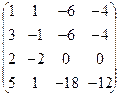 |
| Вариант 29 | Вариант 30 | ||
| Задание 1 | Задание 1 | ||
А = 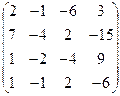 , В = , В = 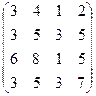 | А = 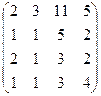 , В = , В = 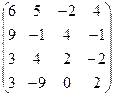 | ||
| Задание 2 | Задание 2 | ||
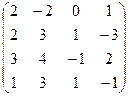 | 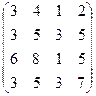 | ||
| Задание 3 | Задание 3 | ||
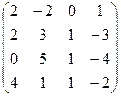 | 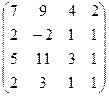 | ||
| Задание 4 | Задание 4 | ||
а) 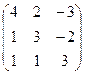 б) б) 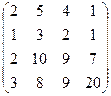 | а) 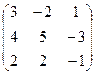 б) б) 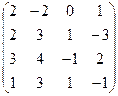 |
Приложение 2. Образец выполнения индивидуального задания
Задание 1. Вычислить выражение A 2+2 AB -5 B T A T, где
A = 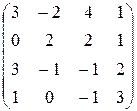 , B =
, B = 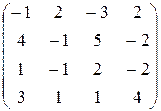 .
.
Решение. Вычислять выражение будем по действиям:
1) A = A × A = 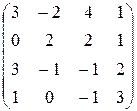 ×
× 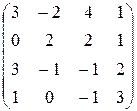 =
= 
= 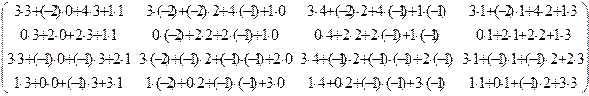 =
=
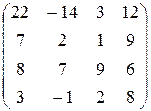
Пояснение: При умножении матрицы на матрицу получается матрица с элементами cij, равными произведениям i -й строки первой на j -й столбец второй. Например, элемент c 23 произведения A × A равен произведению 2-й строки на 3-й столбец:
c 23=0×4+2×2+2×(1)+1×(1)=1.
2) Аналогично,
AB = 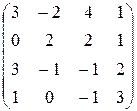 ×
× 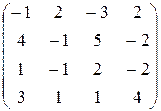 =
=
= 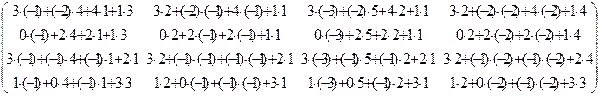 =
=
= 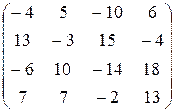 .
.
3) 2 AB =2(AB)=2 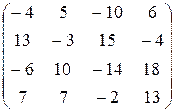 =
= 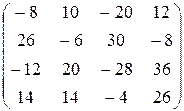 .
.
Пояснение: При умножении матрицы на число каждый элемент матрицы умножается на это число. В нашем случае каждый элемент матрицы AB умножается на число 2.
4) Так как (AB)T= B T A T, то для нахождения B T A T достаточно протранспонировать матрицу AB:
B T A T=(AB)T= 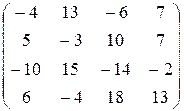 .
.
5) 5 B T A T=5 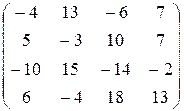 =
= 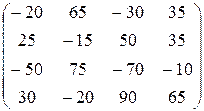 .
.
6) A 2+2 AB -5 B T A T=
= 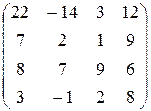 +
+ 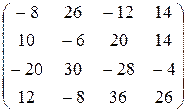 -
- 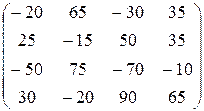 =
=
= 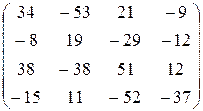 .
.
Ответ: 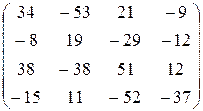 .
.
Задание 2. Найти определитель матрицы
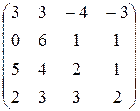 .
.
Решение. Приведём определитель к треугольному виду:
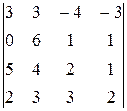
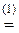 -
- 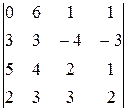
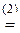
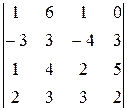
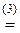
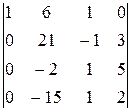
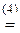
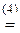 -
- 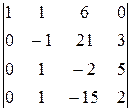
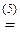 -
- 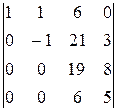
 -
- 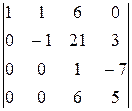
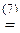 -
- 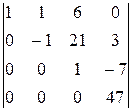
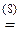 -1×(-1)×1×47=47.
-1×(-1)×1×47=47.
á(1) Поменяли первую и вторую строки местами. Определитель поменял знак на противоположный, не изменившись по абсолютной величине.
(2) Поменяли местами первый и четвёртый столбцы. Снова поменялся знак определителя.
(3) Первую строку, умноженную на 3, прибавили ко второй, умноженную на 2 вычли из четвёртой и просто вычли из третьей.
(4) Поменяли местами второй и третий столбцы.
(5) Вторую строку прибавили к третьей и четвёртой строкам.
(6) Четвёртую строку, умноженную на 3, вычли из третьей.
(7) Третью строку, умноженную на 6, вычли из четвёртой строки.
(8) Определитель треугольной матрицы равен произведению элементов главной диагонали.ñ
Ответ: 47.
Задание 3. Найти ранг матрицы
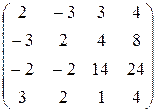
а) методом окаймления миноров;
б) методом элементарных преобразований.
Решение. а) Метод окаймления миноров заключается в том, что на очередном шаге найденный ненулевой минор матрицы окаймляется строкой и столбцом, не содержащими строки и столбцы данного минора. Процесс продолжается до тех пор, пока не найдётся такой порядок r ненулевого минора, что миноры более высоких порядков будут равны нулю. Тогда ранг матрицы будет равен r.
Имеем
M 1= a 11=2≠0.
Окаймляем его второй строкой и вторым столбцом:
M 2= 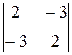 =4-9=-13≠0.
=4-9=-13≠0.
Окаймляем M 2 третьей строкой, и третьим и четвёртым столбцами:
M 3= 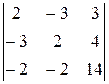 =56+18+24+12-126+16=0,
=56+18+24+12-126+16=0,
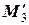 =
= 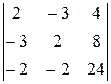 =96+24+48+16-216+32=0.
=96+24+48+16-216+32=0.
Все миноры третьего порядка с участием M 2 и третьей строки равны нулю. В частности, это означает, что все миноры 3-го порядка с участием первой, второй и третьей строк равны нулю.
Продолжаем окаймлять M 2 с участием 4-й строки:
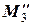 =
= 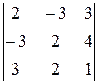 =-93≠0.
=-93≠0.
Среди миноров 3-го порядка есть ненулевой.
Так как все миноры 3-го порядка с участием первых трёх строк равны нулю, то, разлагая минор 4-го порядка по последней строке, получаем, что он равен нулю:
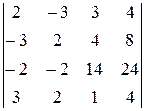 =0.
=0.
Следовательно, rg A =3.
б) Метод элементарных преобразований нахождения миноров заключается в том, что с помощью элементарных преобразований матрица приводится к ступенчатому виду. Число ненулевых строк полученной ступенчатой матрицы равно рангу исходной матрицы.
Имеем
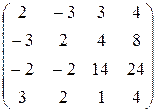
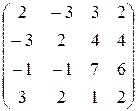
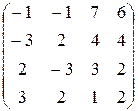
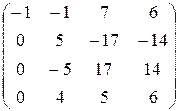
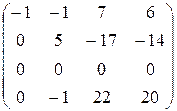
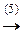
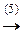
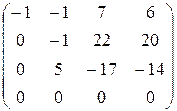
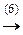
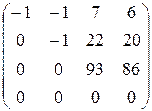
á(1) Третью строку и четвёртый столбец разделили на 2.
(2) Поменяли местами первую и третью строки.
(3) Первую строку, умноженную на 3, прибавили ко второй, умноженную на 2, прибавили к третьей; вторую строку прибавили к четвёртой.
(4) Вторую строку прибавили к третьей и вычли из четвёртой.
(5) Переставили строки местами по схеме 4-я®2-я®3-я.
(6) Вторую строку, умноженную на 5, прибавили к третьей.ñ
В полученной трапециедальной матрице ненулевых строк равно 3. Следовательно, rg A =3.
Задание 4. Найти матрицу, обратную данной двумя методами:
а) 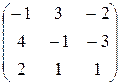 ; б)
; б) 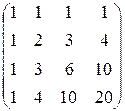 .
.
Решение. а) 1. Найдём A 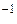 по формуле
по формуле
A 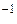 =
= 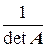
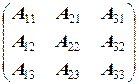 .
.
Имеем
det A = 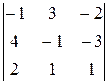 =1-8-18-4-12-3=-44≠0,
=1-8-18-4-12-3=-44≠0,
в частности обратная существует. Найдём алгебраические дополнения Aij элементов:
A 11=(-1)1+1 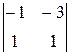 =2; A 21=(-1)2+1
=2; A 21=(-1)2+1 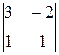 =-5; A 31=(-1)3+1
=-5; A 31=(-1)3+1  =-11;
=-11;
A 12=(-1)1+2 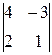 =-10; A 22=(-1)2+2
=-10; A 22=(-1)2+2 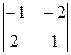 =3; A 32=(-1)3+2
=3; A 32=(-1)3+2 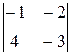 =-11;
=-11;
A 13=(-1)1+3 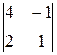 =6; A 23=(-1)2+3
=6; A 23=(-1)2+3 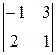 =7; A 33=(-1)3+3
=7; A 33=(-1)3+3 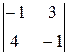 =-11.
=-11.
Поэтому
A 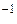 =-
=- 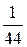
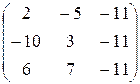 =
= 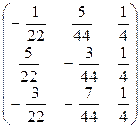 .
.
Проверка:
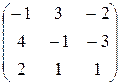 ×
× 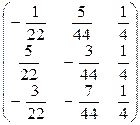 =
= 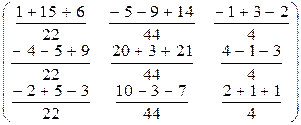 =
=
= 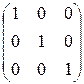 .
.
2. Найдём A 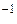 с помощью элементарных преобразований. Он заключается в том, что к матрице A приписывается справа единичная матрица, и полученную матрицу порядка n ´2 n элементарными преобразованиями строк приводим к такому виду, чтобы на месте A получилась единичная. Тогда матрица, полученная на месте единичной, является обратной A
с помощью элементарных преобразований. Он заключается в том, что к матрице A приписывается справа единичная матрица, и полученную матрицу порядка n ´2 n элементарными преобразованиями строк приводим к такому виду, чтобы на месте A получилась единичная. Тогда матрица, полученная на месте единичной, является обратной A 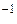 к A. Итак,
к A. Итак,
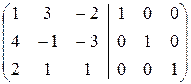
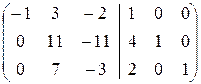
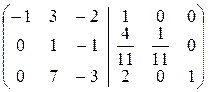
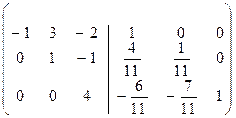
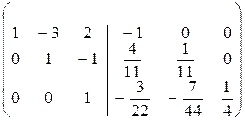
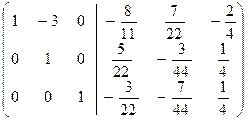
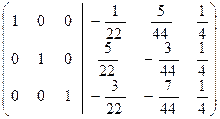 .
.
á(1) Первую строку, умноженную на 4 и 2, прибавили соответственно ко второй и третьей.
(2) Первую и вторую строки разделили -1 и 11 соответственно.
(3) Вторую строку, умноженную на 7, вычли из третьей.
(4) Третью строку разделили на 4.
(5) Третью строку прибавили ко второй и, умноженную на 2, вычли из первой.
(6) Вторую строку, умноженную на 3, прибавили к первой.ñ
Таким образом, на месте приписанной единичной матрицы получили A  .
.
б) 1. Найдём A 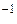 по формуле
по формуле
A 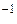 =
= 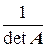
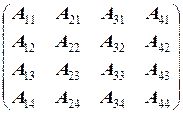 .
.
Имеем
det A = 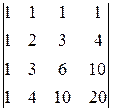
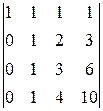
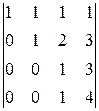
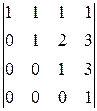
 1≠0,
1≠0,
á(1) Первую строку вычли из второй, вторую - из третьей, третью - из четвёртой.
(2) Вторую строку вычли из третьей, третью - из четвёртой.
(3) Третью строку вычли из четвёртой.
(4) Определитель треугольной матрицы равен произведению диагональных элементов.ñ
в частности обратная существует. Найдём алгебраические дополнения Aij элементов:
A 11=(-1)1+1 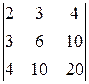
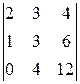
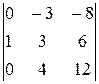
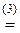 -
- 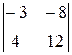 =4,
=4,
á(1) Первую строку вычли из второй и, умноженную на 2, вычли из третьей.
(2) Вторую строку, умноженную на 2, вычли из первой.
(3) Разложили определитель по первому столбцу.
По аналогичной схеме с ведущей первой строкой вычисляем остальные алгебраические дополнения, комментарии к которым опускаем.ñ
A 12=(-1)1+2 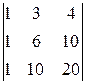 =-
=- 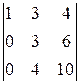 =-3×2
=-3×2 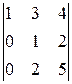 =-6
=-6 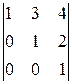 =-6,
=-6,
A 13=(-1)1+3 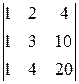 =
= 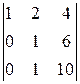 =
= 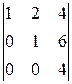 =4,
=4,
A 14=(-1)1+4 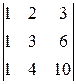 =-
=- 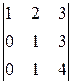 =-
=- 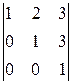 =-1,
=-1,
A 21=(-1)2+1 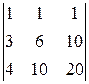 =-
=- 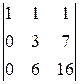 =-
=-  =-6,
=-6,
A 22=(-1)2+2 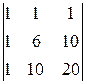 =-
=- 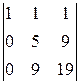 =
= 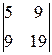 =14,
=14,
A 23=(-1)2+3 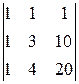 =-
=- 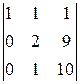 =-
=- 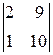 =-11,
=-11,
A 24=(-1)2+4 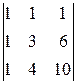 =-
=- 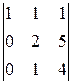 =
= 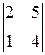 =3,
=3,
A 31=(-1)3+1 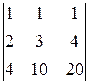 =
= 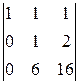 =
= 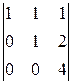 =4,
=4,
A 32=(-1)3+2 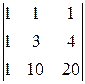 =-
=- 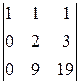 =-
=- 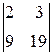 =-11;
=-11;
A 33=(-1)3+3 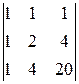 =
= 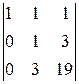 =
= 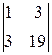 =10,
=10,
A 34=(-1)3+4 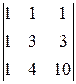 =-
=- 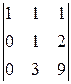 =-3,
=-3,
A 41=(-1)4+1 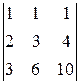 =-
=- 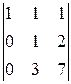 =-
=- 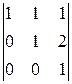 =-1,
=-1,
A 42=(-1)4+2 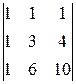 =
= 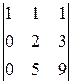 =
= 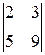 =3;
=3;
A 43=(-1)4+3 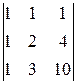 =-
=- 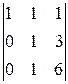 =-
=- 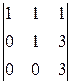 =-3,
=-3,
A 44=(-1)4+4 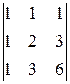 =
= 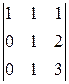 =
= 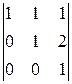 =1,
=1,
Поэтому
A 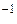 =
= 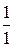
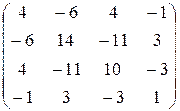 =
= 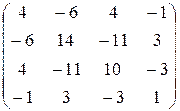 .
.
Проверка:
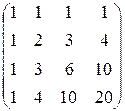 ×
× 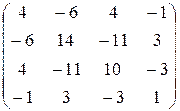 =
=
= 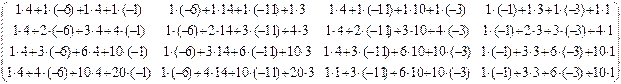 =
=
= 
2. Найдём A  с помощью элементарных преобразований. Как и при вычислении обратной к матрице размерности 3, имеем
с помощью элементарных преобразований. Как и при вычислении обратной к матрице размерности 3, имеем
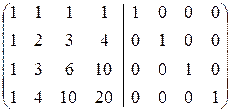
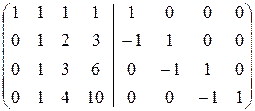
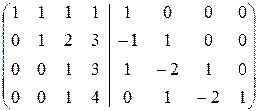
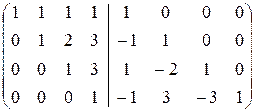
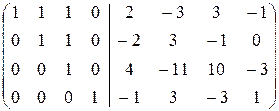
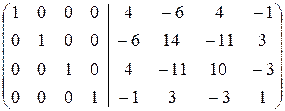 .
.
á(1) Первую строку вычли из второй, вторую - из третьей, третью - из четвёртой.
(2) Вторую строки вычли из третьей и третью - из четвёртой.
(3) Третью строку вычли из последней.
(4) Последнюю строку, умноженную на 3, вычли из третьей, третью вычли из второй и последнюю - из первой.
(5) Вторую строку вычли из первой. ñ
Таким образом, на месте приписанной единичной матрицы получили A 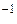 .
.
Ответ: а) 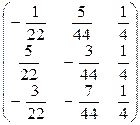 ; б)
; б) 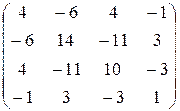 .
.
ЛИТЕРАТУРА
1. Винберг Э.Б. Курс алгебры. ¾ М.: Факториал, 1999.
2. Головина Л.И. Линейная алгебра и некоторые ее приложения. — М.: Наука, 1985.
3. Курош А.Г. Курс высшей алгебры. — М.: Наука, 1971.
4. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1984.
5. Фаддеев Д.К., Соминский И.С. Сборник задач по высшей алгебре. — М.: Наука, 1999.
6. Сборник задач по алгебре/ Под редакцией А.И.Кострикина. — М.: Факториал, 1995.
[1] Ниже в угловых скобках мы приводим комментарии к преобразованиям.
 2015-03-08
2015-03-08 1692
1692