Градиентный метод является одним из основных методов решения задач нелинейного программирования, т.е. поиска минимума некоторой целевой функции.
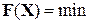 ,
,
где 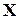 – вектор неизвестных.
– вектор неизвестных.
При решении системы нелинейных уравнений (1) целевая функция формируется как среднеквадратический небаланс узловых токов.
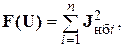
где 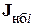 – небаланс тока в i -м узле.
– небаланс тока в i -м узле.
Использование градиентного метода позволяет учесть коэффициенты трансформации – 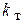 . При этом принимается, что сопротивления трансформаторных ветвей вводятся приведенными к стороне высокого напряжения, а
. При этом принимается, что сопротивления трансформаторных ветвей вводятся приведенными к стороне высокого напряжения, а 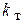 определяется отношением
определяется отношением 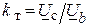 .
.
Действительная и мнимая составляющие тока небаланса определяются из (1)
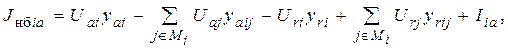
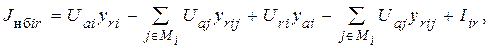
где 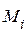 – множество узлов, включая балансирующий, которые имеют непосредственную связь с i -м;
– множество узлов, включая балансирующий, которые имеют непосредственную связь с i -м; 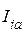 ,
, 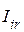 – составляющие узлового тока;
– составляющие узлового тока; 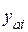 ,
, 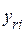 – собственные проводимости узлов;
– собственные проводимости узлов; 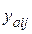 ,
, 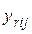 – взаимные проводимости.
– взаимные проводимости.
Все элементы матрицы узловых проводимостей определяются по параметрам ветвей схемы сети с учетом ёмкостной проводимости ЛЭП и коэффициентов трансформации 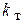 для узлов, соответствующих стороне среднего напряжения автотрансформаторов.
для узлов, соответствующих стороне среднего напряжения автотрансформаторов.
Поиск минимума 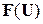 осуществляется в соответствии с алгоритмом, блок-схема которого приведена на рис. 18. Для определения оптимального шага здесь используется пробный шаг
осуществляется в соответствии с алгоритмом, блок-схема которого приведена на рис. 18. Для определения оптимального шага здесь используется пробный шаг 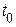 , позволяющий оценить изменение функции в каждой точке в направлении антиградиента.
, позволяющий оценить изменение функции в каждой точке в направлении антиградиента.
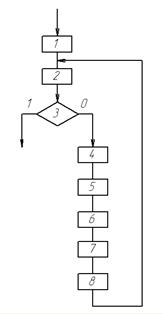 Блоки выполняют следующие функции:
Блоки выполняют следующие функции:
1. Задание исходного приближения 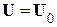 .
.
2. Определение 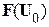 .
.
3. Проверка условия 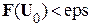 .
.
4. Вычисление градиента 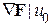 .
.
5. Вычисление 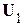 в конце пробного шага
в конце пробного шага 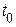 :
:
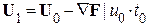 .
.
6. Вычисление градиента в конце пробного шага
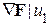 .
.
7. Вычисление оптимального шага
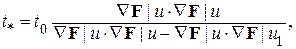
Рис. 18. Блок схема 8. Рабочий шаг 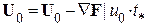 .
.
Составляющая градиента целевой функции по всем неизвестным составляющим узловых напряжений 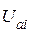 ,
, 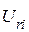 ,
, 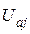 ,
, 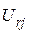 , например,
, например, 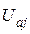 определяется следующим образом
определяется следующим образом
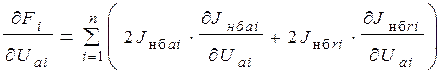 (6)
(6)
Производные небалансов активного и реактивного токов по составляющим напряжений имеют вид:
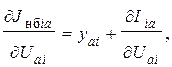
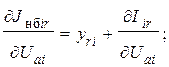
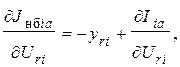
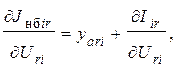
(7)
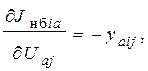
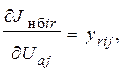
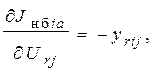
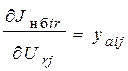
Производные узловых токов можно получить из выражений:
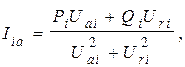
(8)
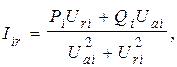
Входящие в (7) производные будут:
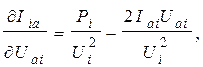
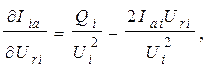 (9)
(9)
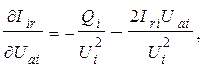
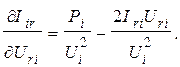
Полученные по (7) с учетом (9) производные являются элементами матрицы 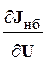 , называемой матрицей Якоби.
, называемой матрицей Якоби.
При разделении векторов 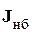 и
и 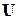 на действительные и мнимые составляющие матрица Якоби разбивается на блочные подматрицы.
на действительные и мнимые составляющие матрица Якоби разбивается на блочные подматрицы.
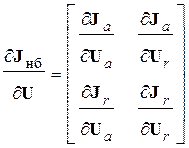
Недиагональные элементы подматриц определяются параметрами системы, причем некоторые проводимости, относящиеся к узлам среднего напряжения автотрансформаторов, зависят от положения отпаек.
Диагональные элементы подматриц определяются параметрами режима, т.е. узловыми мощностями и напряжениями.
Вектор-градиент в текущей точке 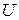 определяется по следующему матричному выражению
определяется по следующему матричному выражению
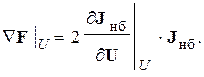
В градиентном методе наиболее эффективны первые шаги. В дальнейшем приближение к точке, являющейся решением, происходит очень медленно.
 2015-03-08
2015-03-08 644
644








